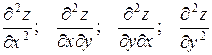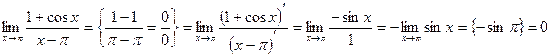Примеры решения задач по математике

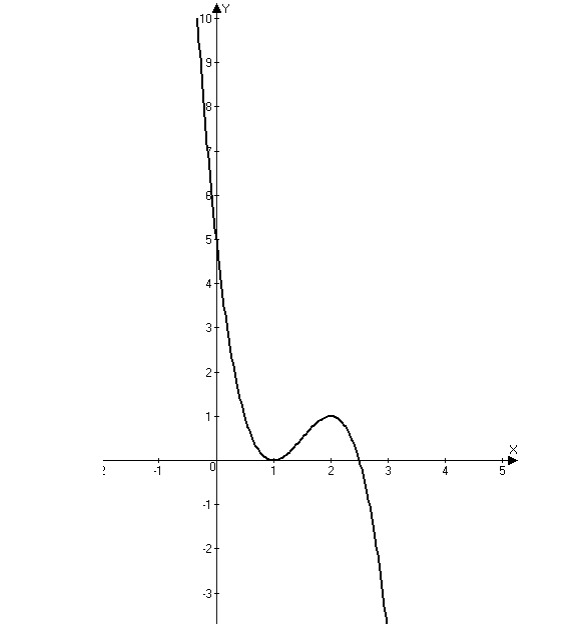
Исследовать функцию методами дифференциального исчисления.

Исследование функции рекомендуется проводить по следующей схеме.

1. Найти область определения функции D(y).
2. Исследовать функцию на четность и нечетность.
3. Найти точки пересечения графика функции с осями координат, если это возможно.
4. Найти интервалы возрастания, убывания и экстремумы функции.
5. Найти интервалы выпуклости и вогнутости, точки перегиба графика функции.
6. По результатам исследования построить график функции.

Решение

Дана функция z=f(x, y).

Найти: а) полный дифференциал функции; б) частные производные второго порядка .

Решение

Дана функция  и  точка .

Найти градиент функции в точке А.

Функция Координаты точки А

Решение

Найти предел, используя правило Лопиталя.

Решение:

Ответ: 0.

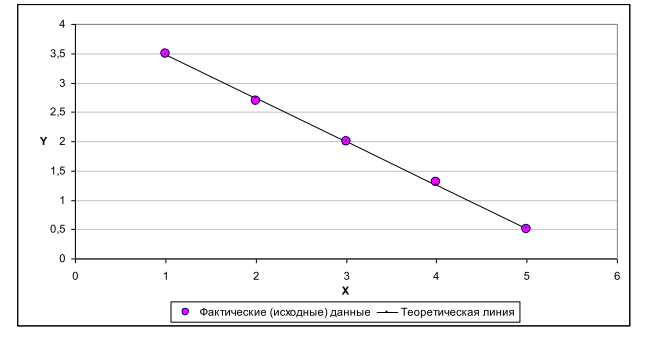
Экспериментально получены пять значений функции y=f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию вида , выражающую приближенно (аппроксимирующую) функцию y=f(x). Сделать чертеж, на котором в декартовой системе координат построить экспериментальные точки и график функции .

Решение