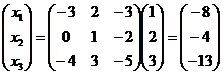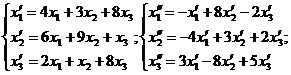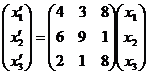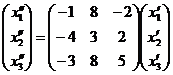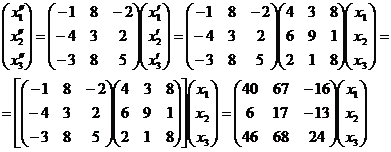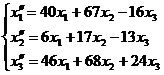1. Даны векторы  в некотором базисе. Показать, что система векторов в некотором базисе. Показать, что система векторов 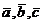 образует базис и найти координаты вектора образует базис и найти координаты вектора 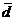 в этом базисе в этом базисе
Решение
Для того, чтобы три трехмерных вектора в трехмерном пространстве образовывали базис необходимо и достаточно, чтобы данная система векторов была линейно независима. То есть коэффициенты в уравнении 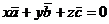 были равны 0. Получаем систему уравнении были равны 0. Получаем систему уравнении
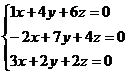
Для того, чтобы эта система имела нулевое решение необходимо и достаточно, чтобы определитель данной системы отличался от нуля.Проверим это:
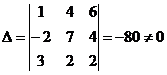 , значит, система векторов является базисом , значит, система векторов является базисом
Найдем коэффициенты разложения вектора 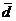 в этом базисе в этом базисе
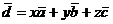 , получаем систему линейных уравнении , получаем систему линейных уравнении
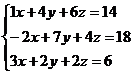
Решим данную систему методом обратной матрицы
Запишем уравнение в виде 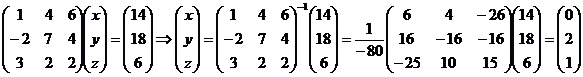 , значит , значит 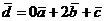
|
|
2. Даны координаты вершин пирамиды 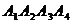 . .
Найти:
1) длину ребра 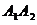 ; ;
2) угол между ребрами 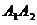 и и 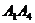 ; ;
3) угол между ребром 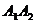 и гранью и гранью 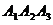 ; ;
4) площадь грани 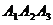 ; ;
5) объём пирамиды;
6) уравнение прямой 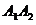 ; ;
7) уравнение плоскости 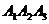
8) уравнение высоты, опущенной из вершины 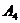 на грань на грань 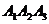
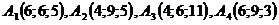 . .
Решение
1)
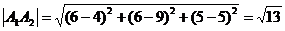
2)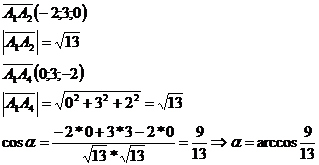
3)
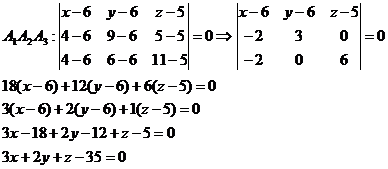
Значит, направляющий вектор плоскости 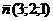
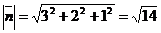
Найдем угол между 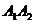 и и 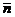
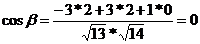 , значит угол между плоскостью и гранью равен , значит угол между плоскостью и гранью равен 
4)
Площадь грани равна половине длины векторного произведения векторов, на которых построена эта грань
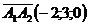
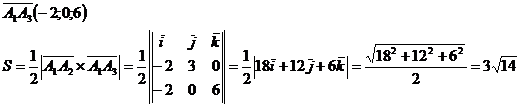
5)
Объем пирамиды равен 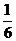 модуля смешанного произведения векторов, на которых построена данная пирамида модуля смешанного произведения векторов, на которых построена данная пирамида
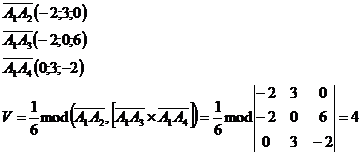
6)
Уравнение прямой 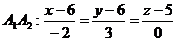
7)
Найдено в пункте 3
8)
Так как направляющий вектор высоты коллинеарен направляющему вектору плоскости и точка 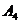 лежит на этой высоте, то уравнение высоты лежит на этой высоте, то уравнение высоты 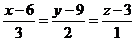 |
|
3. Даны две вершины 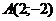 и и 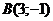 и точка и точка 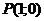 пересечения медиан пересечения медиан 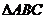 . .
Составить уравнение высоты треугольника, проведенной через третью вершину 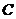 . .
Решение
Координаты точки пересечения медиан есть среднее арифметическое соответствующих координат, то есть
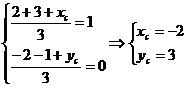
Составим уравнения прямой 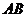
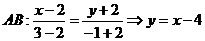
Высота, проведенная через точку С, перпендикулярна прямой 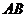 и задается уравнением и задается уравнением 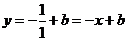 . Константу . Константу 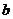 найдем из условия, что точка найдем из условия, что точка 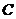 лежит на этой прямой лежит на этой прямой 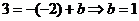 , значит уравнение высоты , значит уравнение высоты 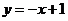 |
|
4. Составьте уравнения линии каждая точка которой одинаково удалена от точки 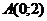 и от прямой и от прямой 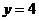
Решение
Пусть 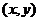 — координаты точки этой линии, тогда — координаты точки этой линии, тогда
Расстояние до прямой 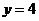 равно равно 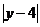
Расстояние до точки 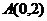 равно равно 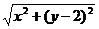
Тогда, исходя из условии задачи, получаем
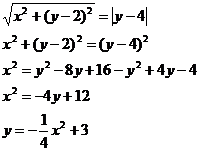
Данная линия представляет собой параболу |
| 5. Дана система линейных уравнений
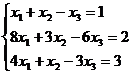
Доказать ее совместность и решить методом Крамера и средствами матричного исчисления.
Решение
Решение данной системы уравнений вычисляется по формулам
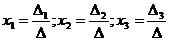 , где , где 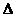 — главный определитель системы, а — главный определитель системы, а 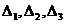 — определители, получающиеся заменой соответственно первого, второго и третьего столбца на столбец свободных членов. — определители, получающиеся заменой соответственно первого, второго и третьего столбца на столбец свободных членов.
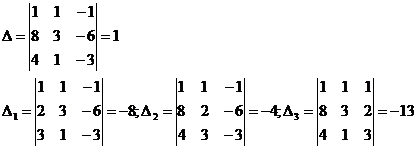
Значит, 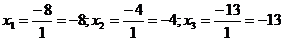
2)
Запишем систему в виде 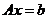 , где , где 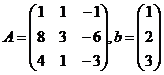 , тогда , тогда 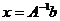 . .
Матрица 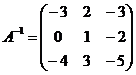 , тогда , тогда 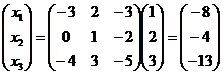 |
| 6. Даны два линейных преобразования
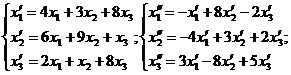
Посредством матричного исчисления найти преобразование выражающее 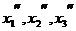  через через 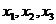
Решение
Из первого преобразования видно, что 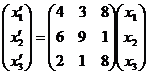
Из второго преобразования видно, что 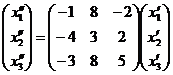
Тогда,
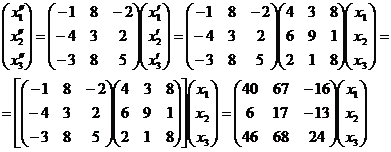
То есть,
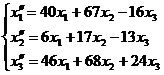
|


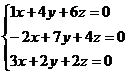
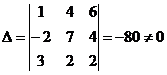 , значит, система векторов является базисом
, значит, система векторов является базисом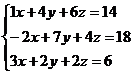
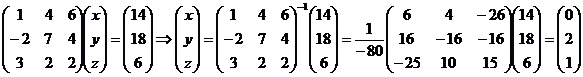 , значит
, значит 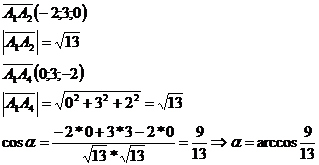
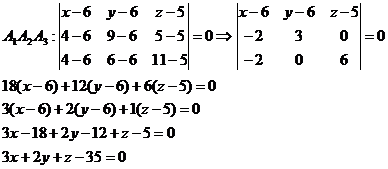
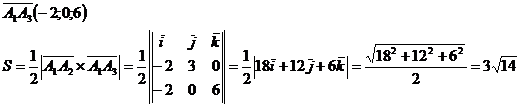
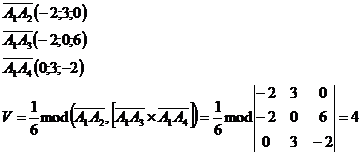
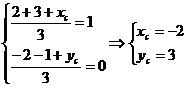
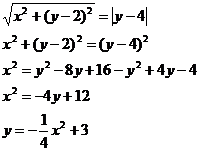
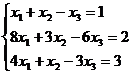
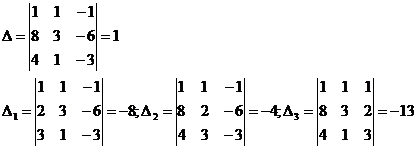
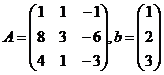 , тогда
, тогда 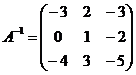 , тогда
, тогда