Примеры решения задач по математике | Страница 4 из 8
35

Примеры решения задач по математике

Примеры по математике
1) Решить систему линейных уравнений по правилу Крамера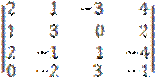
примеры решения задач по математике
Системам линейных уравнений размерность n*n.
В данном случае n=4.
Система имеет вид2×1+x2-3×3+4×4=0
1×1+3×2+2×4=0
2×1-x2+x3-4×4=0
-2×2+3×3-x4=0Метод Крамера:
Для системы вида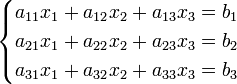
примеры решения задач по математике
Находим определители: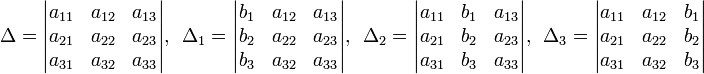
примеры решения задач по математике
И решение будет:
примеры решения задач по математикеВ нашем случае т.т. bi=0, то система имеет одно единственное решение:
x1=x2=x3=x4=0.
Ответ: x1=x2=x3=x4=0.
2) Решить систему линейных уравнений по методу Гаусса: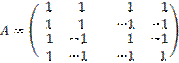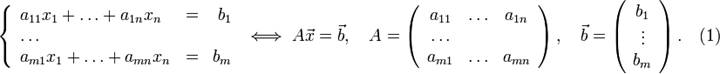
заказать контрольную по математике
заказать контрольную по математикеА – задано, b – предполагаем нулевым.
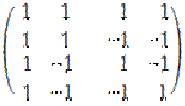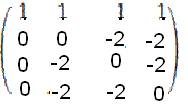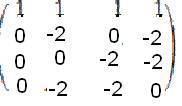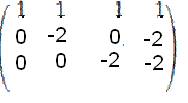Преобразуем А к трапециальному виду:заказать контрольную по математике   вычитаем первую строку из 2, 3 и 4Примеры решения задач по математикеменяем вторую и третью строки местамизаказать контрольную по математикевычитаем вторую стоку из 4ойПримеры решения задач по математике строки 3 и 4 совпадают.
Примеры решения задач по математике
=>
Из 3 строки x3=-x4
Из второй строки x2=-x4
Из первой строки x1=-x4  — x4  +x4  =-x4
=> система имеет бесконечное количество решений удовлетворяющих : (-x4, -x4, -x4, x4)Ответ: бесконечное количество решений удовлетворяющих : (-x4, -x4, -x4, x4)
3) Решить систему линейных уравнений матричным способом. 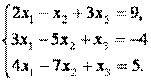Примеры решения задач по математике

AX=B
Примеры решения задач по математикеПримеры решения задач по математике

Примеры решения задач по математике

Примеры решения задач по математике= -10-63-4+60+14+3=0

А – вырожденная матрица, В – ненулевой вектор  => решений нет.
Ответ: решений нет.
4) Решить систему линейных уравнений матричным способом.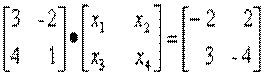
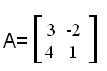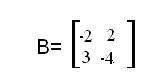Примеры решения задач по математикеОбщий вид системы: АХ=В
Примеры решения задач по математике   Примеры решения задач по математике
Решение системы:
Примеры решения задач по математике
Нахождение обратной матрицы к А:
Примеры решения задач по математикеНаходим определитель матрицы А
detA= 3*1-(-2)*4=3+8=11
Находим союзную матицу: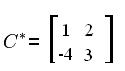
Примеры решения задач по математике
Вычисляем  обратную матрицу: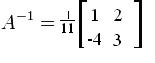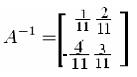
Примеры решения задач по математике примеры решения задач по математикеПримеры решения задач по математике
Находим решенение уравнения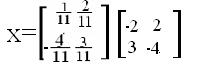
Примеры решения задач по математикепримеры решения задач по математике
x1=1/11*(-2)+2/11*(3)= 4/11
x2=1/11*(2)+2/11*(-4)=-6/11
x3=-4/11*(-2)+3/11*(2)=17/11
x4=-4/11*(3)+3/11*(-4)=-20/11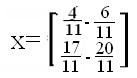Примеры решения задач по математике
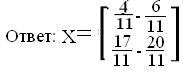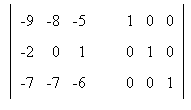x1= 4/11 x2= -6/11    x3= 17/11  x4= -20/11Примеры решения задач по математике
5. Найти обратную матрицу:
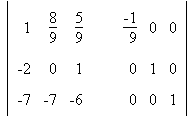Примеры решения задач по математикеСформируем расширенную матрицу:
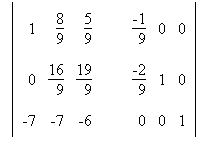Примеры решения задач по математикеРазделим строку 1 на a1,1 = -9
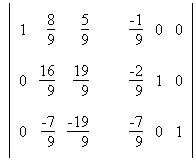Примеры решения задач по математикеВычтем из строки 2 строку 1 умноженную на a2,1=-2
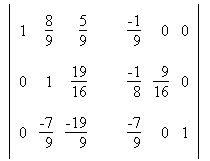Примеры решения задач по математикеВычтем из строки 3 строку 1 умноженную на a3,1=-7
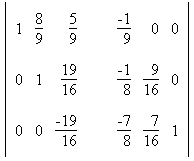Примеры решения задач по математикеРазделим строку 2 на a2,2 = 16/9
Примеры решения задач по математикеВычтем из строки 3 строку 2 умноженную на a3,2=-7/9
Примеры решения задач по математике
Разделим строку 3 на a3,3 = -19/16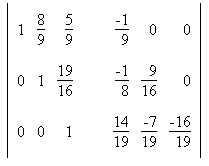
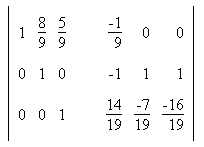Примеры решения задач по математикеВычтем из строки 2 строку 3 умноженную на a2,3=19/16
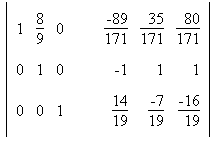Примеры решения задач по математикеВычтем из строки 1 строку 3 умноженную на a1,3=5/9
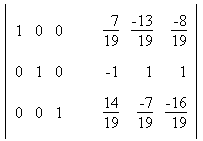Примеры решения задач по математикеВычтем из строки 1 строку 2 умноженную на a1,2=8/9
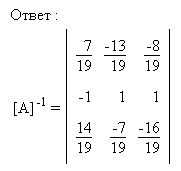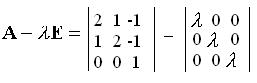Примеры решения задач по математикеВ последней расширенной матрице, левая часть есть единичная матрица, а правая обратная к исходной.Примеры решения задач по математике
6. Найти собственные числа и собственные векторы:
Примеры решения задач по математикеХарактеристическая матрица:
Примеры решения задач по математике
Собственные числа являются решением уравнения: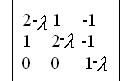
примеры решения задач по математикеНайдем определитель матрицы:
Примеры решения задач по математике(4 — 4Примеры решения задач по математике+Примеры решения задач по математике)(1-Примеры решения задач по математике)-(1-Примеры решения задач по математике)=0
Первый корень Примеры решения задач по математике=1
(1-Примеры решения задач по математике)(3-4Примеры решения задач по математике+Примеры решения задач по математике)=(1-Примеры решения задач по математике)(1-Примеры решения задач по математике)(3-Примеры решения задач по математике)=0
Второй корень совпадает с первым Примеры решения задач по математике=1, третий Примеры решения задач по математике=3Собственные числа Примеры решения задач по математике1=1; Примеры решения задач по математике2=3
Нахождение собственного вектора:
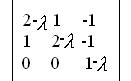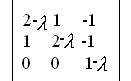Подставим значение: Примеры решения задач по математике1=1
Характеристическую матрицу
Примеры решения задач по математикепримет вид: Примеры решения задач по математике
=>
Найдем собственный вектор примеры решения задач по математике :
Примеры решения задач по математикеПримеры решения задач по математике=0=> Примеры решения задач по математике1+Примеры решения задач по математике2=Примеры решения задач по математике3
Решение составляют вектора Примеры решения задач по математике, которые удовлетворяют Примеры решения задач по математике1+Примеры решения задач по математике2=Примеры решения задач по математике3Подставим значение: Примеры решения задач по математике2=3
Характеристическую матрицу
Примеры решения задач по математикепримет вид: Примеры решения задач по математике
=>
Найдем собственный вектор примеры решения задач по математике :
Примеры решения задач по математикеПримеры решения задач по математике=0=> -2примеры решения задач по математике3=0 =>Примеры решения задач по математике3=0
—Примеры решения задач по математике1+Примеры решения задач по математике2=0
Примеры решения задач по математике1-Примеры решения задач по математике2=0
=>Примеры решения задач по математике1=Примеры решения задач по математике2
Решение составляют вектора Примеры решения задач по математике, которые удовлетворяют Примеры решения задач по математике1=Примеры решения задач по математике2 и Примеры решения задач по математике3=0Ответ: Собственные числа примеры решения задач по математике1=1; примеры решения задач по математике2=3
Собственные вектора:  вектора Примеры решения задач по математике, которые удовлетворяют Примеры решения задач по математике1+Примеры решения задач по математике2=Примеры решения задач по математике3и вектора Примеры решения задач по математике, которые удовлетворяют Примеры решения задач по математике1=Примеры решения задач по математике2 и Примеры решения задач по математике3=0
1 2 3 4 5 6 7 8

Смотрите также:

Первая Мировая война
Реферат Первая Мировая война: предпосылки, ход, итоги
Проектно-сметное дело в нефтяной и газовой промышленности
Пример ответов на билеты управление проектами
Заполняем дневник по практике
Пример заполнения дневника по практике