- Есть вопросы?
- 8(961)1155384
- zakaz@kursach37.com
Математическое программирование для студентов сельхозакадемии
СИММЕТРИЧНЫЕ ДВОЙСТВЕННЫЕ ЗАДАЧИ
1. Двойственность в линейном программировании
Рассмотрим пару задач следующего вида:
| (I) |
(II) |
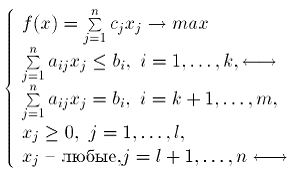 |
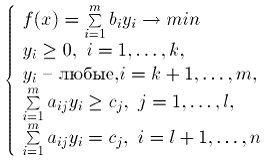 |
Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Но задача, двойственная к (II), есть исходная прямая задача (I). Поэтому можно считать любую из такой пары задач прямой, а другую двойственной. Неравенства задач (I) и (II), соответствующие друг другу, называются сопряженными (они отмечены стрелочками). Множество оптимальных решений задач (I) и (II) будем обозначать DI и DII соответственно.
Для каждой задачи ЛП можно построить двойственную ей задачу по правилам:
1) если прямая задача на максимум, то двойственная ей – на минимум (и наоборот).
2) неравенствам прямой задачи соответствуют неотрицательные переменные двойственной задачи; уравнениям соответствуют переменные, не имеющие ограничения на знак (и наоборот).
Пример 1.
Построить двойственную задачу к следующей задаче линейного программирования
![]() 2×1 – x2 ? 3
2×1 – x2 ? 3
— 3 x1 + 2×2 ? -1
— x1 + x2 = -2
x1 ? 0
Zmax = 5×1 – x2
Так как данная задача на максимум, то двойственная к ней будет задачей на минимум. Однако прежде чем ее строить, необходимо согласовать знаки неравенств в ограничениях задачи с целевой функцией. Задаче на максимум соответствует знак ?, а задаче на минимум ?. Поэтому умножим второе неравенство на (-1). Затем каждому неравенству прямой задачи сопоставим неотрицательную переменную двойственной задачи, а равенству – переменную произвольного знака, и наоборот. Получим пару двойственных задач линейного программирования:
| (I) | (II) |
2×1 – x2 ? 3 — 3 x1 + 2×2 ? -1 — x1 + x2 = -2 x1 ? 0 x2 – любое |
y1 ? 0 y2 ? 0 y3 – любое 2y1 + 3y2 – y3 ? 5 — y1 – 2y2 + y3 = -1 |
Двойственность является одним из фундаментальных понятий в теории линейного программирования. Исключительно важную роль играют следующие утверждения, получившие названия теорем двойственности.
Первая теорема двойственности
Если одна из пары двойственных задач (I), (II) разрешима, то разрешима и другая задач, причем оптимальные значения целевых функций совпадают, т.е. Z(x*) = W(y*), где x* и y* — оптимальные решения задач (I), (II) соответственно.
Говорят, что оптимальные решения x € DI и y € DII удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в любую пару сопряженных неравенств, хотя бы одно из них обращается в равенство.
Вторая теорема двойственности
Решения x € DI и y € DII оптимальны в задачах (I), (II) тогда и только тогда, когда они удовлетворяют УДН.
Пример 2. Задача о распределении ресурсов.
Предприятие планирует использовать отходы основного производства. Для этого намечается выпускать два вида изделий из трех видов ресурсов. Нормы расхода каждого ресурса на единицу продукции каждого вида, запасы ресурсов и доход от реализации единицы товара приведены в таблице:
| Ресурсы |
Затраты ресурсов |
Запасы ресурсов |
|
|
I изд |
II изд |
||
|
1 |
3 |
3 |
15 |
|
2 |
2 |
6 |
18 |
|
3 |
4 |
0 |
16 |
|
Доход |
2 |
3 |
max |
Кроме того, изучение рынка сбыта показало, что объем выпуска изделий I не должен превышать объем выпуска изделий II более, чем на 3 единицы. Какое количество изделий каждого вида должно выпускать предприятие, чтобы суммарный доход был максимален?
Математическая запись задачи ЛП:
![]() 3×1 + 3×2 ? 15
3×1 + 3×2 ? 15
2×1 + 6×2 ? 18
4×1 ? 16
x1 — x2 ? 3
x1 ? 0, x2 ? 0
Zmax = 2×1 + 3×2 Ответ: Zmax = 12, Хопт = (3,2)
Пример 3. Решить двойственную задачу к задаче о распределении ресурсов из примера 2, используя теоремы двойственности.
Выпишем пару двойственных задач.
| (I) | (II) |
| Zmax = 2×1 + 3×2 3×1 + 3×2 ? 15 2×1 + 6×2 ? 18 4×1 ? 16 x1 — x2 ? 3 x1 ? 0 x2 ? 0 |
Wmin = 15y1 + 18y2 + 16y3 + 3y4 y1 ? 0 y2 ? 0 y3 ? 0 y4 ? 0 3y1 + 2y2 + 4y3 + y4 ? 0 3y1 + 6y2 — y4 ? 0 |
Выпишем условия дополняющей нежесткости (УДН), используя каждую пару сопряженных неравенств:
(3х1 + 3х2 — 15)у1 = 0
(2х1 + 3х2 — 18)у2 = 0
(4х1 — 16)у3 = 0
(х1 — х2 — 3)у4 = 0
х1(3у1 + 2у2 + 4у3 + у4 — 2) = 0
х2(3у1 + 6у2 — у4 — 3) = 0
Решение задачи (I) нам известно: Хопт = (3,2) – оптимальное решение, Zmax = 12. По первой теореме двойственности задача (II) также разрешима, причем Zmax = Wmin = 12. Найдем оптимальное решение Уопт = (у1*, у2*, у3*, у4*) задачи (II), используя вторую теорему двойственности. подставим координаты векторов Хопт и Уопт в УДН. Получим:
(3*3 + 3*2 — 15)у1* = 0
(2*3 + 3*2 — 18)у2* = 0
(4*3 — 16)у3* = 0
(1*3 – 1*2 — 3)у4* = 0
3*(3у1* + 2у2* + 4у3* + у4* — 2) = 0
2*(3у1* + 6у2* — у4* — 3) = 0
Так как в третьем уравнении выражение в скобках не равно нулю (4*3 – 16 = -4), то в силу УДН неравенство у3*?0 должно выполняться как равенство, то есть у3*=0. Аналогично получаем у4*=0. Далее, так как х1* = 3, х2*= 2, то в силу УДН 3у1* + 2у2* + 4у3* + у4* — 2 = 0, 3у1* + 6у2* — у4* — 3 = 0.
Получаем систему линейных уравнений:
у4*=0 3у1* + 2у2* + 4у3* + у4* — 2 = 0 3у1* + 6у2* — у4* — 3 = 0 |
у4*=0 3у1* + 2у2* = 2 3у1* + 6у2* = 3 |
у4*=0 у1* = 1/2 у2* = 1/4 |
Решения Хопт = (3,2) € DI и Уопт = (1/2, 1/4, 0, 0) € DII удовлетворяют УДН и, следовательно, в силу второй теоремы двойственности, являются оптимальными в задачах (I) и (II) соответственно.
2. Экономическая интерпретация двойственных переменных и теорем двойственности
Если задача ЛП имеет содержательный экономический смысл, то и двойственная к ней задача также имеет экономический смысл. При этом связь между прямой и двойственной задачами ЛП, устанавливаемая теоремами двойственности, получает содержательную экономическую трактовку.
Рассмотрим задачу о распределении ресурсов и двойственную к ней задачу ЛП. Предположим, что при изучении вопроса об использовании ресурсов появилась возможность их прямой реализации. Спрашивается, какую минимальную цену нужно установить за единицу каждого сырья, чтобы доход от реализации всех видов сырья не был меньше доходов от реализации продукции, которая могла быть выпущена из этого сырья. Обозначим за уi предполагаемую цену i—го сырья. Каждому линейному ограничению первой задачи (то есть каждому ресурсу) ставится в соответствие неотрицательная переменная, i = 1, …, 4. Эти переменные удовлетворяют двум линейным неравенствам, каждое из которых связывает затраты всех ресурсов на производство единицы продукции с величиной получаемого при этом дохода. Так как правые части неравенств задачи (II) измеряются в единицах стоимости, то и левые части должны измеряться в этих же единицах. То есть переменные уi — это некоторые условные цены ресурсов. Линейные ограничения задачи (II) означают, что эти условные цены должны быть такими, чтобы суммарная условная цена всех ресурсов, затрачиваемых на производство единицы продукции, была не меньше дохода от продажи единицы продукции.
Целевая функция W = 15y1 + 18y2 + 16y3 + 3y4 выражает суммарную условную цену всех имеющихся запасов ресурсов. Согласно первой теореме двойственности для оптимальных векторов Хопт = (3,2) и Уопт = (1/2, 1/4, 0, 0) имеет место равенство Z = W = 12, То есть максимальный доход от продажи всей готовой продукции совпадает с минимальной условной ценой всех ресурсов. Оптимальные условные цены указывают, какова наименьшая стоимость ресурсов, дающая возможность обращения этих ресурсов в продукцию.
В силу второй теоремы двойственности оптимальный план Хопти оптимальный вектор условных цен Уоптдолжны удовлетворять УДН. Это означает что:
1) если при производстве продукции в соответствии с оптимальным планом Хопткакой-то ресурс не расходуется полностью ( в нашем примере это ресурсы 3 и 4, так как 4 — 3 = 12 < 16 и 1*3 — 1*2 = 1 < 3. соответственно), то их условные цены равны нулю (у3=0 и у4=0). И наоборот, ресурсы, имеющие ненулевую оптимальную условную цену, используются полностью (из у1*=1/2 и у2*= 1/4 следует, соответственно, 3*3 + 3*2 = 15, 2*3 + 6*2 = 18);
2) если при оптимальном способе производства продукция с номером iвыпускается (в нашем случае и первая, и вторая продукция, так как х1 = 3 > 0, х2 = 2 > 0), то производство этой продукции неубыточно, поскольку суммарные условные цены затрат на производство этой продукции равны доходу от ее реализации (3у1* + 2у2* + 4у3* + у4* — 2 = 0, 3у1* + 6у2* — у4* — 3 = 0). И наоборот, продукция, издержки на производство которой превышают доход от нее, при оптимальном производстве не должна выпускаться, соответствующая переменная хi*
должна быть равна нулю (в нашем примере такая продукция отсутствует).
Дополнительные переменные х3, х4, х5, х6, введенные в задачу (I) при решении симплекс-методом, можно экономически истолковать как количество единиц неизрасходованного сырья соответствующего вида. В оптимальной (последней) симплексной таблице х3 = 0, х4 = 0, поэтому первый п второй ресурсы оптимальным планом расходуются полностью, эти ресурсы дефицитные, и их опенки у1*= 1/2, у2* = 1/4 — положительны. Переменные х5 и х6 не равны нулю (х5 = 4, х6 = 2), третий и четвертый ресурсы расходуются не полностью, они остаются, соответственно, в количестве 4 и 2 единиц. Эти ресурсы недефицитные, их оценки у3*= у4*= 0.



