- Есть вопросы?
- 8(961)1155384
- zakaz@kursach37.com
Математическое программирование для студентов сельхозакадемии
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1. Основные понятия и определения математического программирования
На производстве специалисты часто сталкиваются с проблемой выбора наилучшего варианта решения планово-экономических задач.
Решить эту проблему помогает наука, занимающаяся разработкой теории и методов обоснования выбора наилучших вариантов плана из множества возможных. Она получила название «математическое программирование». Слово «программирование» означает выбор лучшей программы производства, лучшего плана. «Лучший» в зависимости от конкретной цели производства. Цель обязательно выражается количественным показателем (стоимость валовой продукции, сумма затрат и т.д.). Этот показатель называется критерием оптимальности плана и задается математически в виде некоторой целевой функции (функционала). Таким образом, решение планово-экономических задач сводится к нахождению либо максимального, либо минимального значения, другими словами, экстремального значения критерия оптимальности.
В практике наиболее широкое распространение получили планово-экономические задачи, в которых условия производства и критерий оптимальности могут быть представлены в виде системы линейных уравнений и неравенств. Такого рода задачи изучаются в теории линейного программирования — наиболее обширного, хорошо изученного и практически важного раздела математического программирования. Линейное программирование включает общие (симплексный и его модификации) и специальные (распределительный и его модификации) методы.
Под методами линейного программирования понимаются программы математических действий, позволяющие находить оптимальное решение различных экономических проблем, условия решения которых выражены в виде линейных уравнений и неравенств и сведены в единую систему линейных соотношений, подчиненную конкретной целевой функции.
Методами линейного программирования можно решать экономические проблемы, которые удовлетворяют следующим условиям:
- Все экономические, технологические, социальные и другие требования, определяющие оптимальное решение проблемы, должны допускать их математическую формулировку в виде линейных уравнений и неравенств.
- Система линейных соотношений, характеризующая все условия данной проблемы, должна иметь множество допустимых решений, то есть прежде всего сама экономическая проблема должна допускать альтернативные решения.
- Основная цель, которую нужно достичь в результате решения проблемы, должна быть четко выражена экономически и сформулирована в виде линейного соотношения.
Задача линейного программирования может быть представлена в следующих формах:
а) общая – система ограничений представлена неравенствами типа <, >, =; не на все переменные наложены условия неотрицательности; целевая функция может стремиться как к минимуму, так и к максимуму;
б) каноническая (основная) – система ограничений однородна и представлена уравнениями; на все переменные наложено условие неотрицательности (хj?0, j=1…n); целевая функция стремиться к максимуму;
в) стандартная – система ограничений однородна, представлена неравенствами типа < либо =; на все переменные наложено условие неотрицательности; целевая функция стремиться к максимуму или к минимуму.
В настоящее время существует ряд методов решения задач линейного программирования: симплексный метод, метод искусственного базиса (модифицированный симплексный метод или М-метод).
Первой операцией в процессе решения задач симплексным методом является преобразование неравенств в равенства (приведение системы в канонический вид). Делается оно путем введения во все неравенства дополнительных переменных.
Например,
![]() х1 + х2 + 3х3 ? 2 + х4 = 2
х1 + х2 + 3х3 ? 2 + х4 = 2
х1 + 4х2 + 2х3 ? 3 + х5 = 3
2х1 + х2 + 3х3 ? 2 + х6 = 2
хj?0, j=1…n
Эти дополнительные переменные, введенные в соответствии с требованиями алгоритма симплекс-метода, имеют определенный экономический смысл. Дополнительные переменные, введенные в ограничения со знаком ?, обозначают недоиспользование ресурсов (недовыполнение объема ограничений) – недоиспользование пашни, труда и т.д. Дополнительные переменные, введенные в ограничение со знаком ?, означают количество продукта или ресурса сверх минимальной границы (перевыполнение объема ограничений) – плана продаж государству вида продукции.
умение изменять целевую функцию с максимума на минимум
Zmax = — Zmin
если не на все переменные наложено условие неотрицательности, то необходимо уметь преобразовывать отрицательные переменные в неотрицательные
хn = хn’ – хn’’,
где хn’ ? 0,
хn’’ ? 0,
причем хn < 0.
Общие методы линейного программирования (симплексный, М-метод и др.) в принципе дают возможность решить любую задачу, однако, как правило, это решение сопряжено со значительными и трудоемкими расчетами. Поэтому представляет интерес выделение отдельных классов задач, решение которых можно получить с помощью приспособленных для них более простых специальных вычислительных методов. Наиболее широким классом таких задач являются так называемые транспортные задачи. Транспортными задачами называются задачи определения оптимального плана перевозок груза из данных пунктов отправления в данные пункты потребления. Решение транспортных задач осуществляется специальным методом — методом потенциалов (модифицированный распределительный метод или метод «МОДИ»). Он основан на той же идее последовательного улучшения решения, что и симплексный метод, но учитывает специфические свойства математической модели транспортной задачи.
2. Основные понятия и определения математического моделирования
Математическое моделирование может трактоваться как прикладная наука о методах формулирования экономических процессов и явлений, протекающих в производстве.
Математическая модель представляет собой уравнение или систему уравнений, описывающих взаимосвязи, происходящие в оригинале. Предметом изучения курса математического моделирования являются математические методы, применяемые при моделировании процессов и экономических явлений.
Разработка ЭММ осуществляется поэтапно в определенной последовательности. Схематически этот процесс можно представить так:

1 этап — изучение экономического явления по литературным источникам и в натуре и выделение его основных свойств, признаков и зависимостей, характеризующих его.
На этом этапе необходимо выяснить внешние и внутренние связи исследуемого процесса, определить, какие требуются ресурсы, с помощью каких технологических способов ресурсы преобразуются в продукцию.
2 этап — постановка задачи и обоснование критерия оптимальности.
Постановка задачи означает качественный анализ экономического процесса с целью выявления неизвестных параметров, значение которых необходимо определить. При этом важное значение отводится определению конечной цели решения задачи — выбору критерия оптимальности. Он должен отражать как общую цель развития сельскохозяйственного производства, так и конкретное содержание исследуемого экономического явления. Важными сторонами критерия оптимальности являются качественная определенность и количественная измеримость.
3 этап — выбор математического метода решения задачи и базовой математической модели, определение переменных и ограничений задачи.
Данный этап моделирования является обязательным, если ЭММ разрабатывается впервые, когда очень важно определить взаимосвязи исследуемого явления, логику взаимодействия отдельных элементов, установить, каким математическим методом может быть решена эта модель, определить возможность информационного обеспечения модели.
Если же необходимо найти оптимальное решение экономической задачи, для которой уже создана математическая модель и известны методы ее решения, то этот этап можно пропустить и перейти к следующему.
Все рассматриваемые в дальнейшем задачи мы будем решать методами линейного программирования (в частности, симплексным методом) по готовой программе, используя готовые оптимизационные модели, записанные в структурной форме.
Целевая функция достигает экстремума
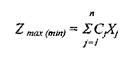
при условии выполнения трех ограничений:
1) по использованию производственных ресурсов — затраты i-го ресурса на производство j-й продукции не будут превышать наличного объема этого ресурса
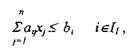
где аij — норма затрат производственного ресурса i-го вида на единицу размерности j-й;
xj — основная переменная;
bi -объем ресурса;
I1 — множество, содержащее номера ресурсов;
2) по заданному объему выполнения работ или производства продукции — объем производства продукции i-го вида в расчете на единицу j-йпеременной будет не меньше гарантированного объема
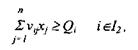
где vij — выход продукции i-го вида с единицы размерности j-й переменной (урожайность, продуктивность);
Qi — гарантированный объем производства i-го вида продукции;
I2— множество, содержащее номера продуктов.
3) условие неотрицательности переменных — поскольку искомые величины являются реальными положительными величинами (посевная площадь, поголовье, объем кормов и т.д.):
Хj > 0 j = 1,…,n.
4 этап — сбор исходной информации и разработка технико-экономических коэффициентов.
Основные требования, предъявляемые к исходной информации, — высокое качество, достаточное количество, соответствующая размерность, достоверность и надежность, своевременность и доступность.
Источниками информации служат годовые отчеты, технологические карты, данные первичного учета, различные нормативные справочники и т.д. Если исходные данные будут недостаточно полными и неточными, то результаты решения задачи могут быть искажены.
Характер исходной информации связан с поставленной планово-экономической проблемой. Если ее решение относится к перспективе, то применяется нормативная, а при решении текущих проблем — нормативная и отчетная информация.
Для любой модели технико-экономические характеристики объекта или процесса формируются в виде технико-экономических коэффициентов аij, коэффициентов целевой функции Cj и констант или объемных показателей ресурсов или продуктов bi. Эти коэффициенты представляют собой основную часть входной информации и их можно подразделить на три группы:
- удельные нормативы затрат или выхода продукции (рассчитываются на основе нормативных справочников, технологических карт, с использованием методов математической статистики и другими способами);
- коэффициенты пропорциональности (коэффициенты при переменных в тех ограничениях, которые предусматривают определенные соотношения между зависимыми переменными по структуре посевов, по поголовью половозрастных групп животных и т.д.);
- коэффициенты связи (когда специально обусловливают зависимость переменной Xj от объемного показателя в ограничении bi, например площадь посева овса не более 100 га).
При подготовке входной информации для ЭММ могут быть использованы производственные функции — математически выраженные связи и зависимости результатов производства от затрат производственных факторов (урожайность культур — от доз внесения удобрений; продуктивность коров — от количества потребляемого корма и т.д.). Помимо прогнозирования уровня результативного признака, производственные функции могут быть использованы для определения экономических оптимумов, коэффициентов эффективности и взаимозаменяемости факторов.
Производственные функции могут быть представлены следующими способами:
- Табличный способ — в виде таблицы, где содержатся ряд значений аргумента и соответствующие значения функции. Этот способ удобен, когда изучают зависимости по опытам и наблюдениям.
- Графический способ — по графику непосредственно выявляются основные свойства представленной функции и весь ход ее изменения.
Преимущество — наглядность.
Недостаток — иногда трудно точно определить значения зависимой переменной у при данных значениях признака х.
3. Аналитический способ — наиболее распространенный — производственная функция представляет собой математическую модель многофакторного экономического процесса, которая позволяет вычислить ожидаемое значение результата производства в зависимости от действующих на него факторов.
В отличие от ЭММ оптимального программирования, состоящих из ряда уравнений и неравенств, модель производственной функции в общем виде в большинстве случаев описывается одним уравнением, где результат производства представляется как функция n независимых факторов:
Х = f(X1, X2,…, Xn)
где Х – производственный результат;
X1, X2,…, Xn– факторы производства.
5 этап — разработка развернутой (матричной) модели экономико-математической задачи.
Модель можно записать развернуто в виде системы неравенств и уравнений, то есть в числовом виде. Однако при достаточно большом числе переменных и ограничений такая запись громоздка, уменьшает обозримость и затрудняет чтение.
Основой развернутой модели является матрица — прямоугольная таблица, в которой записывается развернутая модель задачи в удобной и сокращенной форме.
В матрице по строкам записываются ограничения, а по столбцам -переменные. Все члены одного ограничения должны иметь одну единицу измерения.
Переменные матрицы подразделяются на основные, дополнительные и вспомогательные переменные.
Основные переменные обозначают размер видов или способов Деятельности (площадь посева культур, поголовье скота и т.д.).
Дополнительные переменные вводятся при математической реализации задачи для преобразования неравенств в равенства (прирост кормов, привлечение рабочей силы и т.д.).
Вспомогательные переменные вводятся для определения расчетных величин (для определения общей суммы материально-денежных затрат, показателей эффективности производства и т.д.).
Ограничения матрицы могут налагаться на отдельные переменные, на часть их или на все. По своему характеру ограничения подразделяются на основные, дополнительные и вспомогательные.
К основным ограничениям относятся такие ограничения, которые накладываются на все или большинство переменных и выражают главные, наиболее существенные условия задачи (по использованию производственных ресурсов).
Дополнительные ограничения накладываются на отдельные переменные или на небольшие группы их. Обычно они формулируются в виде неравенств, ограничивающих «снизу» или «сверху» объемы производства отдельных видов продукции, потребление животными отдельных видов или групп кормов и т.д. Особенно важно не перенасыщать модель дополнительными переменными, не сокращать степень свободы системы, иначе решение задачи сведется к арифметическим вычислениям заранее предрешенного результата.
Вспомогательные ограничения не имеют самостоятельного экономического значения. Их используют главным образом для обеспечения правильной формулировки экономических требований (определение вспомогательных переменных).
Ограничения матрицы модели могут иметь разные единицы измерения (площадь посева — га, трудовые ресурсы — чел.-дн.), причем размерность каждого ограничения определяется единицей измерения его правой части. Развернутую числовую ЭММ можно рассмотреть на примере.
Пример:
Составить план сочетания посевных площадей трех культур при условии, что объем земельных ресурсов не должен превышать 900 га, а объем трудовых ресурсов — 5000 чел.-дн. При этом необходимо получить максимум произведенной продукции (ВП) в стоимостном выражении.
Исходные данные
| Культура |
Обозначение (площадь, га) |
Затраты труда, чел.-дн. |
Стоимость ВП, руб. |
| Пшеница |
X1 |
3 |
300 |
| Рожь |
Х2 |
2,5 |
200 |
| Гречиха |
Х3 |
10 |
100 |
Запишем числовую модель:
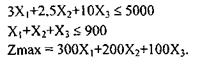
Матрица задачи
| Ограничение |
Ед. изм. |
Обозначение переменных |
Объем и тип ограничения |
||||||
|
Х1 |
Х2 |
Х3 |
… |
… |
?5000 |
||||
| Баланс труда |
чел.-дн. |
3 |
2,5 |
10 |
?900 |
||||
| Баланс пашни |
га |
1 |
1 |
1 |
|||||
| Zmax |
руб. |
300 |
200 |
100 |
|||||
Матрица может иметь блочную структуру. Эта таблица составлена как бы из прямоугольных матриц, обычно расположенных по диагонали. По диагонали рабочей части матрицы стоят рабочие блоки. Каждый блок имеет свои переменные и ограничения. Рабочие блоки связаны между собой связывающим блоком. Такую матрицу имеют задачи по оптимизации состава машино-тракторного парка, размещению сельскохозяйственного производства в размере области или района и т.д.
6 этап — решение задачи на ЭВМ, анализ результатов, корректировка модели, решение задачи с учетом сделанных корректировок.
На этом этапе идет кодирование информации для перенесения на машинные носители и решение задачи на ЭВМ.
7 этап — экономический анализ выполненных расчетов и выбор оптимального варианта плана.
В конкретных условиях в зависимости от характера задачи последовательность этапов моделирования экономических процессов может меняться.
В области сельскохозяйственного производства математическое моделирование используется для решения следующих задач:
- наиболее целесообразного распределения производственных ресурсов (земли, труда, техники и т.д.) в целях максимального увеличения производства сельскохозяйственной продукции;
- достижения заданных объемов производства с минимальными затратами производственных ресурсов;
- эффективного управления производством и наилучшего использования производственных ресурсов при минимальных затратах труда, денежно-материальных средств и времени



