Цифровая электроника

Разделительная дифференцирующая RC-цепь

Электрическая принципиальная схема разделительной дифференцирующей RC-цепи и её временные диаграммы представлены на рис. 2.6.

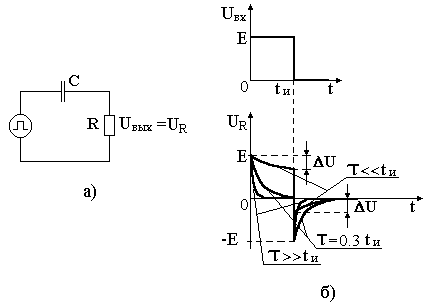
Рис. 2.6. Разделительная дифференцирующая RC-цепь и временные диаграммы напряжений.

Как было показано ранее, меняется по закону:

для 0 ?t ?t_и,

  для t >t_и.

При  рассматриваемая RC-цепь выполняет функции разделительной цепи, назначение которой передать входное напряжение с наименьшими искажениями и отделить при этом постоянную составляющую. Абсолютная величина завала вершины равна напряжению на конденсаторе в момент t_и снятия входного импульса, т.е.

.

Для случая , с учетом рассмотренного ранее разложения функции  при  получаем:

.

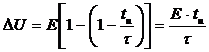Оценкой качества разделительной цепи является величина относительного завала вершины g, которая определяется как:

.

Таким образом, завал вершины, а значит искажение входного импульса, тем меньше, чем больше постоянная времени цепи t при данном t_и. Если величина завала вершины несравненно мала, то импульс передается без искажения.

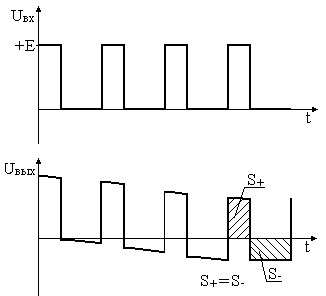
Рис. 2.7. Диаграммы входного и выходного напряжений разделительной цепи.

Из временной диаграммы рис. 2.7 видно, что амплитуда последовательности импульсов выходного напряжения постоянна, но при этом импульсы смещаются относительно нулевого уровня. В установившемся режиме площади под графиком S₊ положительной и S_— отрицательной областей последовательности импульсов окажутся равными друг другу: S₊ = S_—.

Доказать этот факт можно, рассмотрев диаграмму тока, протекающего через резистор (рис.2.8). Очевидно, что i₁t₁ — это заряд Q_и, переносимый через емкость за время действия импульса на входе, а i₂(t₂—t₁) – заряд Q_п, переносимый через емкость за время паузы между импульсами, т.е. в обратном направлении. Тогда общий заряд, переносимый через емкость за время, равное периоду импульса будет равен:

.

Поскольку постоянная составляющая через емкость не проходит , следовательно,  или . Поскольку , а сопротивление – величина постоянная, то значит и равны S₊ и S_— на диаграмме U_вых. Таким образом, для разделительной цепи необходимо выполнение условия: .

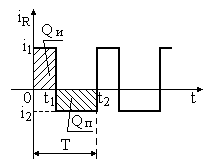
Рис. 2.8. Диаграмма тока, протекающего через резистор разделительной RC-цепи.

Поскольку , а , то

Продифференцируем обе части полученного уравнения. Получим

Так как , то .

Рассмотрим случай . Поскольку , то можно записать . Тогда

.

Из полученной формулы следует название такой цепи – дифференцирующая. Для дифференцирующей цепи должно выполняться условие , т.е. конденсатор должен успевать быстро перезаряжаться при данном t_и. Диаграммы входного и выходного напряжений дифференцирующей цепи для последовательности импульсов представлены на рис. 2.9.

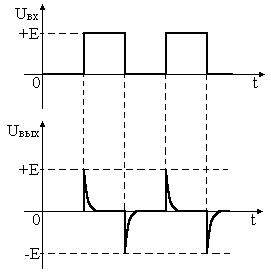
Рис. 2.9. Диаграммы входного и выходного напряжений дифференцирующей RC-цепи.