Цифровая электроника

Интегрирующая RC-цепь

Электрическая принципиальная схема интегрирующей RC-цепи представлена на рис. 2.4(а). Коммутация напряжения на входе, рассмотренная ранее, эквивалентна подаче на вход прямоугольного импульса напряжения (рис. 2.4(б)). Как было выведено ранее, характер изменения функции U_C(t)=U_вых в общем случае выражается следующими зависимостями:

 — нарастающая экспонента для 0 ?t ? t_и;

 — убывающая экспонента для t > t_и, где  — значение напряжения, до которого успел зарядиться конденсатор в период действия импульса.

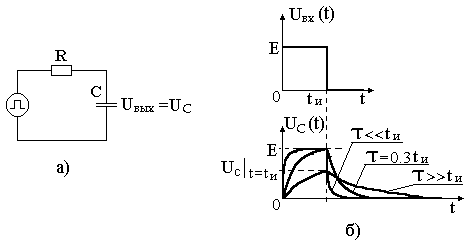
Рис. 2.4. Интегрирующая RC-цепь и временные диаграммы напряжений.

Разряд конденсатора после прекращения действия импульса приводит к тому, что выходной импульс будет иметь большую продолжительность, чем входной. Происходит расширение импульса без сохранения его формы, поэтому такая RC-цепь называется расширяющей.

Поскольку, а , то

.

Так как , то

.

Рассмотрим случай, когда . Поскольку , следовательно , и можно записать:

,

то есть на выходе интеграл от входного напряжения. Отсюда очевидно название рассмотренной цепи – интегрирующая. Эта цепь используется, в частности, для получения линейно изменяющегося напряжения. Для этого на вход интегрирующей цепи подается постоянное напряжение . Тогда получаем

,

то есть на выходе линейно изменяющееся напряжение (рис. 2.5).

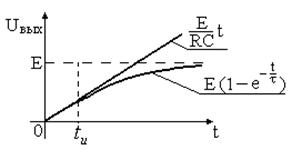
Рис. 2.5. Графики изменения идеального и реального выходных напряжений интегрирующей RC-цепи.

В отличие от рассмотренного идеального случая, в реальной цепи

.

Найдем производную по t от функции идеального выходного напряжения:

.

Аналогично для функции реального выходного напряжения производная запишется:

.

При t=0  ,

т.е. в нуле производные реальной и идеальной функций совпадают, а в дальнейшем — расходятся. За меру расхождения на интервале [0, t_и] принимают коэффициент нелинейности  — относительное изменение производной:

.

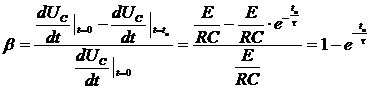Для случая  можно воспользоваться формулой разложения функции :  при . Тогда

,

т.е. чем больше t при данном значении t_и, тем меньше ?. Реальная функция U_вых.р в этом случае ближе к идеальной U_вых.ид.