Цифровая электроника

Переходные процессы в RC-цепях

Процессы, протекающие в простейшей RC-цепи

Переходный процесс обусловлен тем, что энергия электромагнитных полей, связанных с цепью при различных установившихся режимах различна, а скачкообразное изменение энергии, т.е. изменение энергии на конечную величину за бесконечно малый промежуток времени, невозможно из-за ограниченности величины мощности физически существующих источников энергии.

Линейным устройством (элементом) называется устройство (элемент), параметры которого не зависят от протекающего тока или приложенного напряжения. Нелинейное устройство — это устройство, параметры которого зависят от тока или напряжения.

Переходные процессы в простейших линейных цепях, т.е. в цепях RL или RC описываются дифференциальным уравнением первого порядка:

,

где x(t) — напряжение или ток в схеме, y(t) — внешнее воздействие.

Решение этого уравнения для случая y(t) = const имеет вид:

,

где t — текущее время, x(t) — напряжение или ток в схеме, x(?) — конечное значение x(t) при t®?, x(0) — начальное значение x(t) при t = 0.

Характер изменения функции x(t) представлен на рис. 2.1 (убывающая или нарастающая экспонента).

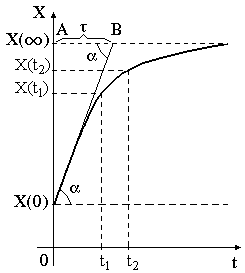
Рис. 2.1. Характер изменения экспоненциальной функции.

Выполним следующие преобразования:

,

.

Поскольку , то очевидно, что AB = t.

При анализе переходных процессов часто возникает задача нахождения интервала времени , за который функция x(t) изменяется от значения x(t₁) до значения x(t₂). Запишем значение функции в точках t₁ и t₂:

,

.

Откуда

,

,

,

,

.

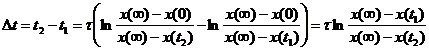Применим полученные соотношения для анализа RC-цепей. Предварительно напомним законы коммутации для RL и RC-цепей:

1-ый закон коммутации: напряжение на конденсаторе в момент коммутации не может измениться скачком U_С(0_—) = U_С(0₊);

2-ой закон коммутации: ток, протекающий через индуктивность, не может измениться скачком I_L(0_—) = I_L(0₊).

Законы коммутации являются следствием того, что энергия в цепи не может изменяться мгновенно, так как для этого требуется бесконечно большая мощность источников энергии. Рассмотрим RC-цепь (рис. 2.2).

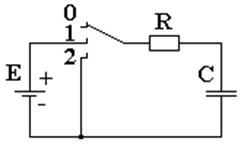
Рис. 2.2. Схема простейшей RC-цепи.

Пусть конденсатор не заряжен и в момент времени t = 0 ключ переходит из положения «0» в положение «1». Для начальных и установившихся режимов в этом случае можно записать:

при t = 0 U_С(0) = 0, U_R(0) = E;

при t = ? U_С(?) = E, U_R(?) = 0.

После подстановки получаем:

,

.

Считая, что конденсатор заряжен до значения U_С = E, рассмотрим процесс после перевода ключа из положения «1» в положение «2». Начальные и установившиеся значения напряжений на элементах в этом случае запишутся:

при t = 0 U_С(0) = E,U_R(0) = -E;

при t = ? U_С(?) = 0, U_R(?) = 0.

После подстановки получаем:

,

.

Характер изменения функций U_C(t) и U_R(t) представлен на рис. 2.3.

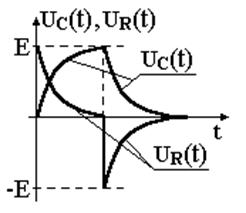
Рис. 2.3. Характер изменения функций U_С(t) и U_R(t) простейшей RC-цепи.

Из курса математики известно, что за утроенное значение постоянной времени, т.е. за время 3t, экспонента изменяется на 0.95 своего конечного полного изменения. Это значит, что за время 3t конденсатор условно разряжается и заряжается.