Цифровая электроника

Определение функции алгебры логики

Для анализа и синтеза цифровых электронных схем широко используется математический аппарат алгебры логики, или булевой алгебры, разработанной в середине XIX века ирландским математиком Дж. Булем. Основным понятием алгебры логики является понятие переключательной функции или булевой функции алгебры логики (ФАЛ). Функцией алгебры логики nпеременных называется такая функция, которая принимает только два возможных значения — 0 или 1, как и переменные, от которых эта функция зависит. Для nпеременных возможно 2ⁿ различных значений переключательной функции f. Если заданы все 2ⁿ значений функции, то она называется полностью определенной. Если же часть значений функции f не задана, то такая функция носит название неопределенной или частично определенной.

ФАЛ задаются таблично (в виде так называемых таблиц истинности), аналитически (в виде алгебраических выражений), в виде последовательности десятичных чисел или в виде кубических комплексов. В таблице 1.3 приведен пример табличного задания произвольной функции трех переменных f=f(A,B,C).

Таблица 1.3.

Конкретная комбинация значений аргументов носит название набора. Каждый набор имеет индекс j, численно равный десятичному эквиваленту двоичного числа.

ФАЛ от одной и двух переменных принято называть элементарными. Эти функции имеют специальные названия и обозначения и используются при воспроизведении более сложных логических функций. В таблице 1.4 приведены все возможные переключательные функции двух переменных.

Таблица 1.4.

Для аналитической записи переключательных функций используются вспомогательные функции, называемые конституентой единицы и конституентой нуля. Конституентой единицы n переменных называется такое булево произведение (конъюнкция) этих переменных, в которое каждая переменная входит только один раз в прямой или инверсной форме.

Переменная, принимающая на данном наборе единичное значение, записывается в конституенте единицы в прямом виде, а отрицательное – в инверсном виде. Отличительной особенностью конституенты единицы является то, что она равна «1» только на одном, вполне определенном наборе значений переменных. Будем обозначать конституенту единицы символом m_j, где индекс jуказывает на номер набора, на котором конституента единицы становится равной «1». Аналогично конституента нуля есть булево сложение (дизъюнкция) nлогических переменных, которое обращается в «0» лишь при одном наборе аргументов. При этом в прямом виде в конституенте нуля будет записываться переменная, принимающая на данном наборе нулевое значение, а в инверсном – единичное значение.

Аналитическая запись функции осуществляется по таблице истинности. Непосредственно из данных таблицы находится так называемая совершенная дизъюнктивная нормальная форма булевой функции (СДНФ) по выражению:

,

где f_j — значение функции на j-ом наборе, m_j — конституента единицы, равная «1» только на одном j-ом наборе, U — символ логического сложения (дизъюнкции), аналогичный символу алгебраического сложения .

Для записи выражений в совершенной конъюктивной нормальной форме (СКНФ) используют формулу:

,

где f_j— значение функции на j-ом наборе, n_j — конституента нуля, равная «0» только на одном j-ом наборе, U — символ логического произведения (конъюнкции), аналогичный символу алгебраического произведения O.

Проиллюстрируем СДНФ и СКНФ переключательной функции на примере булевой функции 3-х переменных, заданной таблицей 1.3. Формула для любой СДНФ функции 3-х переменных будет иметь вид:

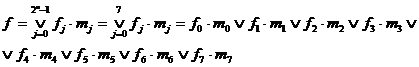
Подставляя из таблицы значения функций f₀f₇, получаем:

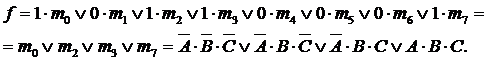
Формула для любой СКНФ функции 3-х переменных будет иметь вид:

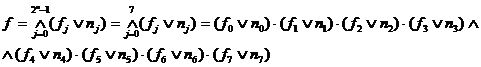
Подставляя из таблицы значения функций f₀f₇, получаем:

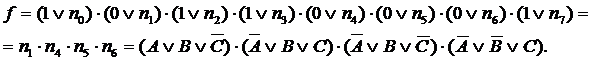
Аналогично находятся СДНФ и СКНФ любой другой булевой функции, заданной таблично.

Аналитическая запись ФАЛ, а также ее дальнейшие тождественные преобразования с целью получения оптимального вида опираются на следующие основные законы и тождества алгебры логики:

• переместительный закон XY=YX, XY=Y>X;
• сочетательный закон X(YZ)=(XY)Z, X(YZ)=(XY)Z;
• распределительный закон X(YZ)=XYXZ,XYZ=(XZ)(YZ);
• закон отрицания (правило де Моргана) , ;
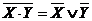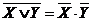• закон двойного отрицания ;
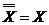• закон идемпотентности X>X=X, 1X=1, 0X=X,XX=X, 1X=X, 0X=0;
• закон склеивания X, ;
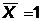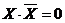• закон поглощения YXX=X; (YX)X=X

• константы

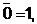
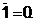
Иногда вместо аналитической формы используют запись логической функции в виде последовательностей десятичных чисел. Такая запись является аналогом таблиц истинности и СДНФ или СКНФ, но при этом является гораздо более компактной. При этом в скобках указывают десятичные эквиваленты двоичных кодов конституент единицы или нуля, или, что одно и то же, номера наборов функции f, в которых она принимает единичные или нулевые значения. При указании номеров наборов с единичными значениями функции перед скобкой слева указывается знак дизъюнкции  или , а с нулевыми – знак конъюнкции  или . В качестве примера запишем функцию, заданную таблицей 1.3 в виде десятичных чисел на единичных и нулевых наборах:

f(A,B,C)=(0,2,3,7)=(0,2,3,7);

fAB,C=(1,4,5,6)=(1,4,5,6).

В случае автоматизированного проектирования логических схем электронных цифровых устройств на ЭВМ ФАЛ удобно записывать в виде кубических комплексов. Такая форма в силу ограниченного числа символов позволяет формализовать запись логических функций большого числа переменных. Каждый набор переменных представляется в виде n-мерного вектора, где n– количество входных переменных. Вершины этого вектора образуют вершины n-мерного куба. Если функция задана тремя переменными, то она образует трехмерный куб, который легко представляется геометрически в виде объемной фигуры. Все единичные вершины куба, в которых функция fпринимает значение «1», образуют множество нулевых кубов, называемое нулевым кубическим комплексом К₀. Нулевой кубический комплекс записывается набором двоичных кодов входных переменных, для которых функция принимает единичные значения. Вершины, расположенные на концах ребер куба, называютсясоседними и отличаются только одной переменной. Если два куба, для которых функция равна «1», являются соседними, то они образуют куб более высокого порядка. Так, если два нулевых куба комплекса К₀являются соседними, т.е. отличаются только одной переменной, то они образуют единичный куб, геометрически представляющий ребро исходного n-мерного куба. Набор единичных кубов образуют единичный кубический комплекс К₁. Записывается единичный кубический комплекс в виде набора двоичных кодов совпадающих переменных, а вместо несовпадающих проставляются прочерки. Аналогично соседние единичные кубы, отличающиеся только одной переменной, образуют двоичные кубы, набор которых в свою очередь образуют двоичный кубический комплекс К₂и т.д.

Рассмотрим запись ФАЛ в виде кубических комплексов на примере функции, заданной таблицей 1.3. Поскольку функция определяется тремя переменными, то ее можно представить трехмерным кубом (рис. 1.1). Вершины этого куба сформированы таким образом, чтобы каждая переменная, входящая в уравнение, располагалась в одной оси базиса трехмерного пространства X-Y-Z. В оси Х располагается переменная А, в оси>Y – переменная Ви в оси Z – переменная С. Окружностями отмечаем вершины куба, в которых функция принимает значения единицы. Эти вершины (нулевые кубы) образуют нулевой кубический комплексК₀=(000, 010, 011, 111). Из рисунка наглядно видны соседние вершины, в которых нулевые кубы отличаются только одной переменной. Ребро исходного куба, образованное соседними вершинами, выделяем толстой линией. Эти ребра образуют единичные кубы, в записи которых вместо несовпадающих переменных ставятся прочерки. Набор единичных кубов образует единичный кубический комплекс К₁=(0-0, 01-, -11).

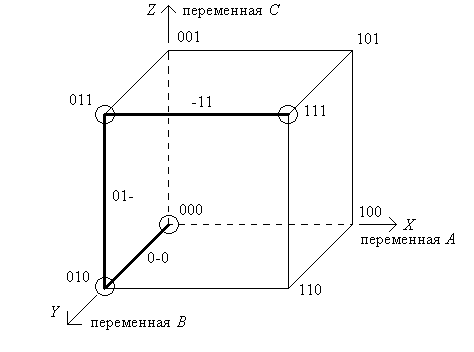
Рис. 1.1.Кубические комплексы функции, заданной таблицей 1.3.

Единичный кубический комплекс для рассмотренного выше примера является максимально возможным. Для некоторых произвольных функций трех переменных может оказаться возможным выделение двоичных кубов, образующих двоичный кубический комплекс К₂. Геометрически такие кубы образовывают грани исходного трехмерного куба. В записи двоичных кубов будет присутствовать значение одной совпадающей переменной и два прочерка для несовпадающих, например, (-1-). Для функции n переменных существует теоретическая вероятность нахождения (n-1) кубических комплексов. Совокупность всех кубических комплексов образует кубический комплекс ФАЛ: К(f)=(К₀, К₁, …, К_m), где m – максимально возможный кубический комплекс функции n переменных.

Для выражения ФАЛ от многих переменных достаточно иметь ограниченное число разнотипных элементарных переключательных функций, называемое системой. Как показано выше, любая функция алгебры логики может быть записана в виде СДНФ или СКНФ. Следовательно, любую функцию аргументов можно представить с помощью системы только из трех элементарных функций: инверсия, дизъюнкции и конъюнкции.

Система функций алгебры логики называется функционально полной, если любая функция от произвольного числа аргументов n может быть представлена с помощью этих функций. Полная система функций называется базисом. Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций, образующих этот базис, превращает систему функций в неполную. Так, полная система из дизъюнкции, конъюнкции и инверсии может быть сокращена, поскольку с помощью формул де Моргана можно представить либо конъюнкцию через инверсию и дизъюнкцию, либо дизъюнкцию через инверсию и конъюнкцию. Таким образом, базис из дизъюнкции, конъюнкции и инверсии не является минимальным. Поскольку ни дизъюнкция, ни конъюнкция не могут быть выражены через инверсию и наоборот, то базисы, состоящие из инверсии и дизъюнкции и из инверсии и конъюнкции, являются минимальными.

Возможны различные базисы и минимальные базисы, отличающиеся числом входящих в них функций и их видом. Приведем примеры функционально полных систем:

• конъюнкция, дизъюнкция, инверсия;
• конъюнкция, инверсия;
• дизъюнкция, инверсия;
• стрелка Пирса;
• штрих Шеффера.

Выбор минимального базиса связан с выбором стандартного набора логических элементов, из которых будет строиться конкретное цифровое устройство. Очевидно, что уменьшение числа функций, входящих в базис, соответствует уменьшению числа различных логических элементов, принятых за стандартные. Однако уменьшение типов стандартных элементов может привести к увеличению их общего числа. Таким образом, сложность цифрового устройства зависит не только от вида реализуемой функции, но и от вида функций, выбранных в качестве базиса.