Цифровая электроника

Счетчики

Счетчики представляют собой последовательностые цифровые устройства и предназначены для выполнения операций счета и хранения кода числа подсчитанных импульсов. Существуют различные схемы счетчиков, отличающихся назначением, типом используемых триггеров, организацией связи между ними, порядком смены состояний. По порядку изменения состояний счетчики бывают с естественным и произвольным порядком счета. В первых значение кода каждого последующего состояния счетчика отличается на единицу от кода предыдущего состояния. В счетчиках с произвольным порядком счета значения кодов соседних состояний могут отличаться более чем на единицу. Счетчики также подразделяются на простые и реверсивные. Простые счетчики делятся на суммирующие и вычитающие. В суммирующих счетчиках код последующего состояния имеет большее значение, чем код предыдущего состояния, а в вычитающих – меньшее значение. Реверсивные счетчики могут работать как в режиме суммирования, так и в режиме вычитания.

Основными параметрами счетчика являются:

• модуль счета или коэффициент пересчета К_сч;
• быстродействие счетчика.

Модуль счета К_сч характеризует число устойчивых состояний счетчика, т. е. предельное число импульсов, которое может быть им сосчитано. После поступления К_сч входных импульсов счетчик возвращается в исходное состояние. Такие счетчики называются также делителями на число, равное К_сч.. По модулю счета счетчики подразделяются на двоичные, у которых К_сч=2^m, и недвоичные, у которых К_сч?2^m, где m – положительное целое число.

Быстродействие счетчика в свою очередь определяется двумя величинами:

• разрешающей способностью 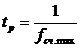, т.е. минимальным допустимым интервалом времени между подачей двух входных импульсов, при котором не происходит потеря счета;
• временем установки t_уст кода счетчика, т.е. интервалом времени между моментом поступления входного сигнала и моментом завершения перехода счетчика в новое устойчивое состояние.

При этом должно выполняться условие t_р>t_уст.

Поскольку счетчики представляют собой класс ПЦУ, то и синтез их целесообразно выполнять на основе базовых элементов ПЦУ, т.е. триггерах. Количество триггеров для двоичных счетчиков определяется формулой

m_дв.=log₂K_сч.

Для недвоичных счетчиков количество триггеров следует выбирать из условия

m_недв.=[log₂K_сч],

где [log₂K_сч]- двоичный логарифм заданного коэффициента пересчета, округленный до ближайшего (большего) целого числа.

Двоичные счетчики. Начнем с двоичных счетчиков. Для их построения можно использовать различные типы триггеров. Наиболее удобным является триггер Т-типа (счетный триггер), который осуществляет подсчет импульсов по модулю 2. Такой триггер по сути дела является простейшим счетчиком с К_сч=2. Соединив несколько счетных триггеров определенным образом, можно получить схему многоразрядного счетчика. Если в качестве базовых используются Т-триггеры с прямым динамическим счетным входом, то для построения трехразрядного суммирующего двоичного счетчика, их необходимо объединить так, как это показано на рис. 5.14,а. Срабатывание всех триггеров происходит по переднему фронту счетного импульса. Поэтому, чтобы реализовать операцию суммирования, необходимо на триггеры Т2 и Т3 информацию подавать с инверсных выходовпредыдущих триггеров. Временная диаграмма работы счетчика показана на рис. 5.14,б.

Состояния выходов Q₁, Q₂ и Q₃ сгруппируем в зависимости от номера счетного импульса в таблице 5.1. Из таблицы очевидно, что двоичный код, задаваемый логическими состояниями выходов счетчика соответствует порядковому номеру входного счетного импульса С. При подаче последнего восьмого импульса счетчик возвращается в исходное состояние, после чего процесс повторяется. Модуль счета, таким образом, К_сч=2³=8.

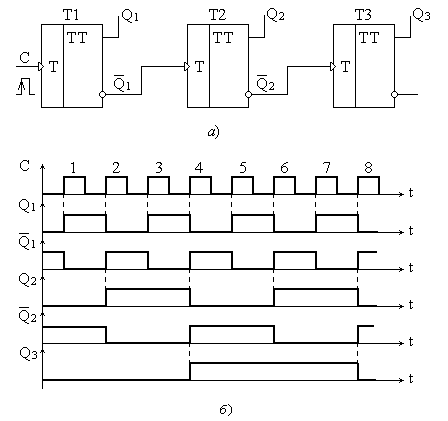
Рис. 5.14.Структурная схема и временная диаграмма работы трехразрядного двоичного суммирующего счетчика на основе Т-триггеров с прямым динамическим счетным входом.

Таблица 5.1.

Суммирующий счетчик можно построить и на базе Т-триггеров с инверсным динамическим счетным входом. При этом, поскольку срабатывание триггеров происходит по заднему фронту счетного импульса, нет необходимости задействовать инверсные выходы  этих триггеров. Сигнал на вход каждого последующего триггера необходимо подавать с прямого выхода предыдущего триггера (рис. 5.15,а). При этом необходимо учитывать, что срабатывание всего счетчика будет происходить по заднему фронту счетного импульса С, как это показано на временной диаграмме рис. 5.15,б.

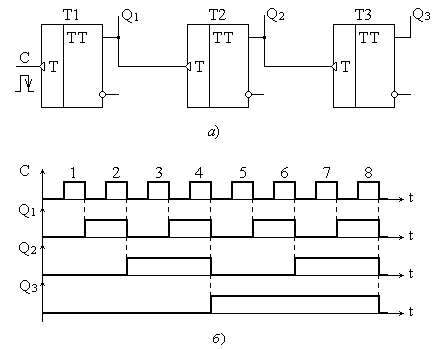
Рис. 5.15. Структурная схема и временная диаграмма работы трехразрядного двоичного суммирующего счетчика на основе Т-триггеров с инверсным динамическим счетным входом.

Для выполнения операции вычитания достаточно изменить в электрических связях соответствующих схем используемые выходы триггеров на выходы с обратными логическими уровнями, либо использовать триггеры с входами обратного типа динамического управления. Если вычитающий счетчик реализуется на базе Т-триггеров с прямым динамическим входом, то сигналы на входы последующих триггеров, в противоположность схемы рис. 5.14,а, необходимо подавать с прямых выходов предыдущих триггеров (рис. 5.16,а). Временная диаграмма работы счетчика с такой структурой приведена на рис. 5.16,б. Из временной диаграммы видно, что с каждым последующим счетным импульсом выходной код уменьшается на единицу (декрементируется). С последним восьмым импульсом счетчик возвращается в исходное состояние.

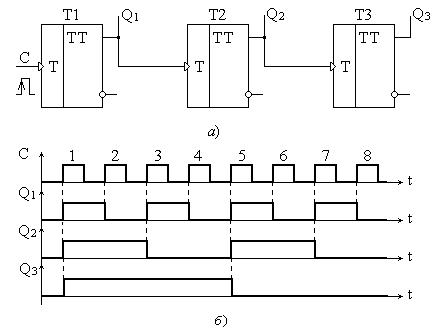
Рис. 5.16. Структурная схема и временная диаграмма работы трехразрядного двоичного вычитающего счетчика на основе Т-триггеров с прямым динамическим счетным входом.

Таким образом, путем переключения выходов с инверсных на не инверсные и обратно, можно получить как суммирующие, так и вычитающие счетчики. Это свойство положено в основу построения реверсных счетчиков. Для этих целей используются коммутаторы выходов на базе логических элементов 2И-ИЛИ-НЕ (рис. 5.17). Элементы ЛЭ1 и ЛЭ2 выполняют роль коммутаторов выходных сигналов с триггеров Т1 и Т2. При подаче логического нуля на вход «-1» и логической единицы на вход «+1», на выходе верхней структуры И элементов ЛЭ1 и ЛЭ2 формируется результат с выходов Q₁ и Q₂ соответствующих триггеров. На выходе нижней структуры И присутствует логический нуль, в результате чего выходы  и  не влияют на работу схемы. Структура ИЛИ-НЕ элементов ЛЭ1 и ЛЭ2 инвертирует значения соответствующих коммутируемых выходов. Таким образом, осуществляется инверсия сигналов Q₁ и Q₂, которые подаются на прямые динамические тактовые входы триггеров Т2 и Т3. Счетчик работает в режиме суммирования. При подаче логического нуля на вход «+1» и логической единицы на вход «-1» картина меняется. Закрытыми оказываются прямые выходы Q₁, Q₂, а открываются инверсные выходы  и . При этом, их значения инвертируются элементами ИЛИ-НЕ ЛЭ1 и ЛЭ2, в результате чего они становятся прямыми. Счетчик начинает работать в режиме вычитания. На практике, с целью упрощения процесса управления, обычно вместо двух входов «+1» и «-1» используется только один из этих входов. Сигнал второго входа формируется через инвертор.

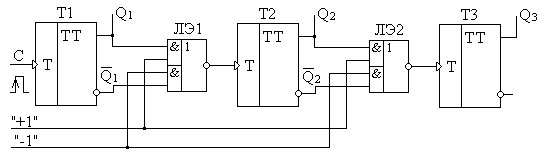
Рис. 5.17.Структурная схема трехразрядного двоичного реверсивного счетчика.

В рассмотренных счетчиках срабатывание триггеров происходит поочередно друг за другом, т.е. последовательно. Такие счетчики называются асинхронными. Их недостаток состоит в том, что увеличивается общее время установления t_уст с увеличением числа триггеров. Кроме того, появление промежуточных комбинаций может привести к ложному срабатыванию дешифратора, если такой есть в структуре ПЦУ. Для устранения этого недостатка используются счетчики, у которых все триггеры срабатывают одновременно. Такие счетчики получили название синхронных счетчиков. Идея синхронного счетчика заключается в построении внешней комбинационной схемы, формирующей сигналы, согласно которым будет происходить одновременное переключение только части триггеров в зависимости от текущего выходного кода. Причем эти сигналы должны быть сформированы до поступления очередного счетного импульса. Счетный импульс должен поступать на все триггеры одновременно. Для этих целей необходимо использовать тактируемые Т-триггеры, входы синхронизации которых объединяются в общую шину. На тактовые Т-входы каждого триггера подаются заранее сформированные сигналы переноса с комбинационной схемы.

Анализ смены состояний суммирующего счетчика показывает, что если значение младшего разряда меняется каждый раз с приходом входного сигнала, то в остальных разрядах значение будет меняться на противоположное только в тех случаях, когда до этого во всех предыдущих разрядах были единицы. Для этого единичный входной сигнал должен поступать на вход триггера только в том случае, если триггеры во всех предыдущих разрядах находятся в единичном состоянии. Задачу формирования входного сигнала для каждого последующего триггера выполняет логический элемент И ЛЭ1 (ЛЭ2), на входы которого подаются сигналы со всех выходов предыдущих триггеров (рис. 5.18). Срабатывание всех триггеров происходит одновременно по общему сигналу синхронизации С, который является счетным импульсом для всего счетчика. Изображенная на рисунке структура называется счетчиком с параллельным переносом, поскольку сигналы на все элементы И, формирующие единичные переносы, подаются с выходов триггеров одновременно в параллельном виде. В исходном состоянии на выходах всех триггеров присутствуют логические нули. С поступлением каждого счетного импульса выходные коды начинают увеличиваться на единицу (инкрементироваться). Задержка в такой схеме равна времени срабатывания одного триггера.

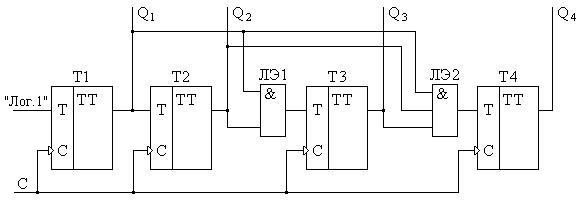
Рис. 5.18. Структурная схема четырехразрядного суммирующего счетчика с параллельным переносом.

Чтобы синтезировать схему вычитающего счетчика, необходимо использовать не прямые, а инверсные выходы триггеров. Таким образом, в исходном состоянии все триггеры будут иметь на инверсных выходах логические единицы. С началом счета выходные коды будут уменьшаться (декрементироваться). Используя принцип коммутации прямых или инверсных выходов триггеров, можно также реализовать реверсивный счетчик с параллельным переносом.

Недостатком счетчиков с параллельным переносом является необходимость использования в случае увеличения разрядности счетчика элементов И с большим числом входов. При этом выходы триггеров должны обладать высокой нагрузочной способностью. Поэтому многоразрядные счетчики строят по групповому принципу. Согласно этому принципу, весь счетчик структурно реализуется путем соединения отдельных групп небольшой разрядности с параллельным переносом внутри этих групп. Сигнал переноса из очередной группы формируется элементом И, объединяющим выходы всех триггеров данной группы. Сформированный сигнал переноса предыдущей группы подается на счетный вход последующей группы. Общая задержка такого счетчика определяется суммой задержек каждой группы.

Другой вариант структуры синхронного счетчика – это структура со сквозным переносом. Согласно этой структуре, перенос формируется только из единичных результатов соседних разрядов. Для этих целей достаточно использовать только двухвходовые элементы И при любой разрядности счетчика (рис. 5.19). Перенос между разрядами осуществляется через каждый элемент И (ЛЭ1 и ЛЭ2) в их последовательной структуре. Отсюда следует, что общее время срабатывания всего счетчика определяется временем срабатывания одного триггера и суммарным временем задержки последовательной цепи логических элементов И. Выигрыш по быстродействию в такой структуре осуществляется за счет меньшего времени срабатывания одного логического элемента по сравнению со временем срабатывания одного триггера. При достаточно большой разрядности счетчика, время задержки во всех элементах И может оказаться значительным и сравняться с временем срабатывания одного триггера.

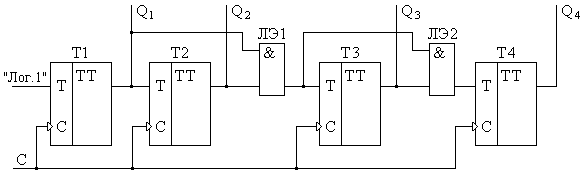
Рис. 5.19. Структурная схема четырехразрядного суммирующего счетчика со сквозным переносом.

Недвоичные счетчики. Недвоичные счетчики имеют К_сч?2^m. Принцип их построения заключается в исключении некоторых устойчивых состояний обычного двоичного счетчика. Избыточные состояния исключаются с помощью обратных связей внутри счетчика. Как было показано ранее, количество триггеров в недвоичном счетчике есть округленное до большего целого числа значение m_недв=[log₂K_сч]. Поэтому, если задействовать все возможные состояния m триггеров, то счетчик окажется двоичным. Организуя обратные связи в двоичном счетчике таким образом, чтобы определенными выходными кодовыми комбинациями осуществлять либо его обнуление, либо установку в состояние, отличное от очередного, реализуется недвоичный счетчик с произвольным К_сч. Часть состояний двоичного счетчика, таким образом, пропускаются.

Наибольший интерес среди недвоичных счетчиков представляют двоично-десятичные счетчики с К_сч=10, которые строятся на основе четырех счетных триггеров. Важность этого класса счетчиков заключается в том, что с их помощью легко может быть осуществлен вывод содержимого счетчика в десятичном коде. Действительно каждый двоично-десятичный счетчик имеет десять устойчивых состояний и соответствует одному разряду десятичной системы счисления.

В условном графическом обозначении функция двоичного счетчика определяется символами «СТ». В случае, если счетчик не двоичный, то рядом с этими символами проставляется цифра, соответствующая модулю счета. В маркировке микросхем функция счетчика кодируются символами «ИЕ».