Цифровая электроника

Дешифраторы и шифраторы

Дешифратор – это устройство, предназначенное для преобразования двоичного кода в напряжение логической единицы (логического нуля) на том выходе, номер которого совпадает со значением двоичного кода на входе. При n входах в полном дешифраторе имеется 2ⁿ выходов, т.е. для каждой комбинации входных сигналов имеется соответствующий выход. Дешифратор, у которого при n входах число выходов меньше 2ⁿ, называется неполным. Другое название дешифратора — декодер. Принцип работы полного трехразрядного дешифратора рассмотрим на примере его таблицы истинности.

Соответствующие таблице истинности ФАЛ имеют вид

.

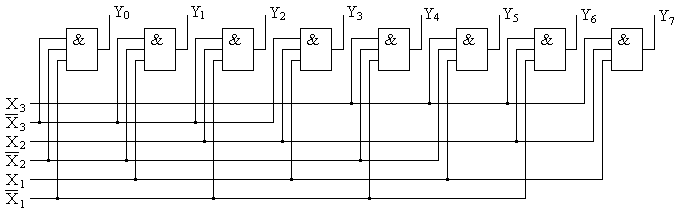
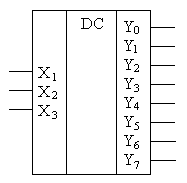
Структурная схема трехразрядного дешифратора, синтезированная на основании полученных ФАЛ приведена на рис. 4.10,а, а его УГО — на рис. 4.10,б.

б)

Рис. 4.10.Структурная схема и УГО трехразрядного дешифратора.

В общем случае логические уравнения для выходных переменных дешифратора n-разрядного числа имеют вид

………

.

Построенные по полученным формулам дешифраторы называются линейными. К преимуществу линейных дешифраторов можно отнести высокое быстродействие, поскольку входные переменные одновременно поступают на все элементы И. Одновременно, без дополнительных задержек, формируется и результат на выходах этих элементов. Очевидно, что для реализации линейного дешифратора n-разрядного числа необходимо иметь 2ⁿ логических элементов И с n-входами. В существующих микросхемах логических элементов количество входов ограничено. Следовательно, ограничена и разрядность реализуемых на их основе линейных дешифраторов, что является недостатком. Кроме того, недостатком является и то, что предыдущие элементы, работающие на входы дешифратора, должны иметь высокую нагрузочную способность, т.е. должны быть рассчитаны на подключение большого числа логических элементов И. Каждый из входов дешифратора подключен к 0,5·2ⁿ логическим элементам И. Поскольку нагрузочная способность базовых логических элементов ИС не превышает величины N=10?20, то максимальная разрядность дешифрируемых чисел для линейных дешифраторов n=4?5.

Указанного недостатка лишены пирамидальные дешифраторы. Принцип построения этих дешифраторов состоит в том, что сначала строят линейный дешифратор для двухразрядного числа X₁, X₂, для чего необходимы 2²=4 двухвходовые схемы И. Далее, каждая полученная конъюнкция логически умножается на входную переменную X₃ в прямой и инверсной форме. Полученная конъюнкция снова умножается на входную переменную X₄ в прямой и инверсной форме и т.д. Наращивая таким образом структуру, можно построить пирамидальный дешифратор на произвольное число входов. На рис. 4.11 приведена структура пирамидального дешифратора для трех разрядов.

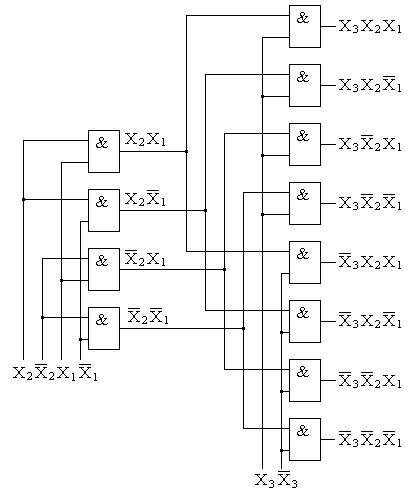
>Рис. 4.11. Пирамидальный дешифратор для трехразрядного числа.

Характерным отличием пирамидальных дешифраторов от линейных является использование только двухвходовых логических элементов вне зависимости от разрядности дешифрируемого числа. В то же время количество логических элементов в пирамидальном дешифраторе больше. Однако следует иметь ввиду, что количество логических элементов, располагаемых в одном корпусе ИС, определяется главным образом требуемым количеством выводов. Следовательно, в одном корпусе ИС можно расположить большее число двухвходовых элементов, чем трехвходовых, четырехвходовых и т.д. И значит, пирамидальная структура дешифратора по числу корпусов ИС может оказаться более предпочтительной, чем линейная.

Шифраторы выполняют задачу обратную той, которую выполняют дешифраторы: появление логической единицы (логического нуля) на определенном входе приводит к появлению соответствующей кодовой комбинации на выходе. Также как и дешифраторы, шифраторы бывают полными и неполными. Работа восьмивходового полного шифратора задается следующей таблицей истинности:

На основании таблицы истинности можно записать ФАЛ, задающие работу восьмивходового шифратора:

.

Синтезированная на основании приведенных логических уравнений структурная схема шифратора представлена на рис. 4.12,а, а его условное графическое обозначение – на рис. 4.12,б.

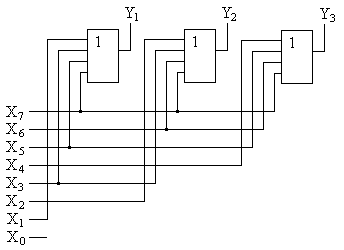
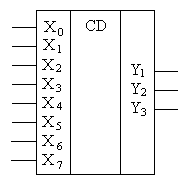
а)  б)

Рис. 4.12.Структура и УГО восьмивходового шифратора.