Цифровая электроника

Сумматоры

Сумматоры – это класс КЦУ, выполняющих операцию арифметического сложения двух двоичных n-разрядных чисел. Сумматоры бывают полными и неполными. Неполный сумматор или полусумматор — это комбинационное устройство с двумя входами и двумя выходами, выполняющее операцию сложения двух одноразрядных чисел в соответствии с таблицей истинности, где А и В – входные одноразрядные числа, S_п/см. – выход суммы, а P_п/см. – выход переноса в старший разряд:

Записанные по таблице истинности ФАЛ для переменных S_п/см. и P_п/см. имеют вид

,

.

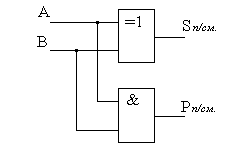
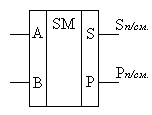
Первое уравнение для S_п/см. обозначает операцию Исключающее ИЛИ (Сложение по модулю два), а второе — для P_п/см. – операцию логической конъюнкции. Поскольку во всех сериях микросхем имеются элементы Исключающее ИЛИ, то структурную схему полусумматора удобно синтезировать на основе именно этого элемента и элемента И (рис. 4.6,а). Условное графическое обозначение полусумматора приведено на рис. 4.6,б.

а)  б)

Рис. 4.6.Структурная схема и УГО полусумматора.

Полный одноразрядный сумматор выполняет операцию арифметического сложения двух одноразрядных чисел A и B с учетом переноса из младшего разряда Р_-1. Он имеет три входа и два выхода. Работа полного одноразрядного сумматора задается таблицей истинности:

Записав СДНФ для переменных S и P и выполнив ряд тождественных преобразований можно получить следующие ФАЛ для полного сумматора:

,

.

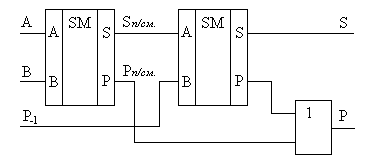
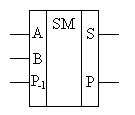
Выражение  есть ни что иное, как значение выхода переноса полусумматора над величинами S_п/см. и Р_-1. Учитывая этот факт и анализируя полученные логические уравнения, можно сделать заключение о возможности реализации полного сумматора на основе двух полусумматоров и одного элемента ИЛИ. Структура полного одноразрядного сумматора представлена на рис. 4.7,а, а его УГО – на рис. 4.7,б.

а) б)

Рис. 4.7. Схема и УГО полного одноразрядного сумматора.

Из таблицы истинности полного одноразрядного сумматора очевидно, что на выходе суммы S формируется единица, а на выходе переноса Р – нуль при наличии единицы на одном из входах A, B или Р_-1. При наличии единиц на любых двух из трех входов полного сумматора, на выходе S будет нуль, а на выходе P – единица. При наличии на всех трех входах логических единиц, на обоих выходах сумматора присутствуют единицы. При нулях на всех трех входах выходы также принимают нулевые состояния. Структура, реализующая описанное правило и положенная в основу микросхем сумматоров 155 и 555 серий, приведена на рис. 4.8.

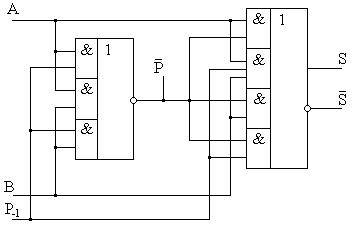
Рис. 4.8.Структурная схема одноразрядного полного сумматора, положенная в основу микросхем ТТЛ-типа.

При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их необходимо соединить в последовательные структуры. Выходы переноса Р микросхем младших разрядов подключаются к входам переноса Р_-1 микросхем старших разрядов. Отдельные разряды слагаемых подаются на входы А и В микросхем соответствующих разрядов, а с их выходов S снимаются разряды результата суммирования. Выход переноса P микросхемы самого старшего разряда является выходом переноса результата суммирования всего n-разрядного числа.

Такой способ наращивания разрядности сумматоров путем последовательного объединения нескольких полных сумматоров меньшей разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие. Распространение переноса в таких структурах осуществляется последовательно от микросхемы к микросхеме. Этого недостатка лишены сумматоры с параллельным переносом. Выражение для переноса в старший разряд одноразрядного полного сумматора можно преобразовать к следующему виду

Введем обозначения  и , где g_i – функция переноса, h_i – функция передачи переноса. Тогда

.

В общем случае можно записать

,

где  — перенос в самый младший разряд из предыдущего сумматора, если таковой предусмотрен в структуре цифрового устройства. В противном случае =0. Таким образом, сигнал p_i можно получить одновременно с появлением всех разрядов а_i и в_i на входах сумматора, не дожидаясь формирования переноса в отдельных разрядах полных одноразрядных сумматоров. В случае четырехразрядных чисел А и В можно записать

,

,

.

Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные ФАЛ для p_i каждого разряда реализовать в каком-либо базисе, например И-НЕ. Далее выходные сигналы p_i с каждой части такой комбинационной схемы должны быть поданы на соответствующие входы Р_-1 полных одноразрядных сумматоров. Пример такой структуры приведен на рис. 4.9.

Из рисунка видно, что даже для четырехразрядного сумматора требуется достаточно сложная комбинационная схема формирования переноса. Поэтому схемы сумматоров с параллельным переносом реализуют обычно для сложения чисел с разрядностью не более четырех бит.

При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей разрядности используют два подхода. Первый заключается в использовании полных сумматоров с параллельным переносом в качестве базовых элементов и объединении их в общую последовательную структуру. Сумматоры, реализованные по такой структуре, называются сумматорами с цепным переносом. Подобная структура не может обладать максимальным быстродействием, но при этом является простой в схемотехнической реализации.

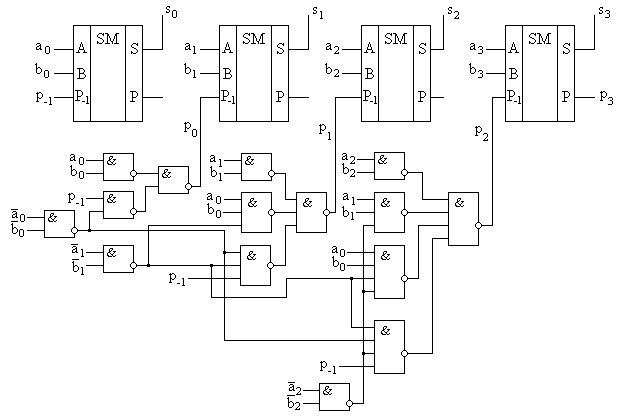
Рис. 4.9. Схема четырехразрядного сумматора с параллельным переносом.

Второй подход также основан на использовании набора сумматоров с параллельным переносом. Но их объединение в общую структуру основано на принципе параллельной передачи переноса. В этом случае требуется дополнительная комбинационная схема, реализующая параллельный перенос между параллельными сумматорами. Сумматоры с такой структурой называются параллельно-параллельными. Они имеют максимальное быстродействие, но их реализация требует дополнительных аппаратных затрат.