Исследование систем управления

ОБЩЕНАУЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ

КОЛИЧЕСТВЕННЫЕ МЕТОДЫ

ПАРАМЕТРИЧЕСКИЙ МЕТОД ИССЛЕДОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ

Параметрический метод основывается на количественном и качественном описании исследуе­мых свойств СУ (объекта исследования) и установлении взаимосвя­зей между параметрами как внутри управляющей и управляемой подсистем, так и между ними. Это позволяет с помощью заранее избранной номенклатуры параметров на базе фактических данных количественно оценить исследуемый объект. Зависимости между параметрами могут быть как функциональными, так и корреляционными.

Каждая СУ обладает рядом специфических свойств, позволяю­щих отличить ее от любых других. Свойство СУ — объективная осо­бенность системы, проявляющаяся при ее создании и функциони­ровании.

Свойства будущей СУ формируются и учитываются при состав­лении задания на проектирование и непосредственно при самом проектировании. При создании новой системы эти свойства реализуются и конкретизируются. В процессе эксплуатации происходит проявление и поддержание свойств СУ. Чем сложнее СУ, тем более сложным комплексом свойств она обладает, тем сложнее формы их проявления.

Свойства могут быть простыми и сложными. Простое свойство это, например, численность управленческого персонала, срок служ­бы технических средств управления и др. Примером сложного свойства может служить производительность труда управ­ленцев, которая включает объем выполняемых функций и числен­ность персонала.

Любое свойство системы можно охарактеризовать словесно, чис­ленно, графически, в виде таблицы, функции, т.е. с помощью его при­знаков.

Признак — отличительная черта, характерная для какой-либо совокупности объектов. Примером качественных признаков могут служить тип ОСУ, метод управления, метод оценки СУ, способ рас­чета численности персонала и т.п. Существенным значением среди качественных признаков обладают альтернативные признаки, которые имеют только два взаимоисключающих варианта, например, наличие или отсутствие ошибок в работе персонала. Помимо качественных альтернативных признаков свойств СУ могут быть признаки многовариантные.

Для объективной оценки любой системы необходи­мо количественно охарактеризовать ее свойства. Количественную характеристику свойств объ­екта исследования дают параметры. Частным случаем параметра СУ является показатель — количе­ственная характеристика существенных свойств системы, значимых для ее существования и функционирования. Следовательно, параметр системы сле­дует воспринимать как более широкое понятие, так как он может характеризовать любые свойства системы или ее компонентов.

Качественные признаки также могут влиять на вид функцио­нальной зависимости показателей СУ от ее параметров. Например, используемый метод распределения функций управления в подразделении, являющийся качественным призна­ком, оказывает существенное воздействие на зависимость уровня качества выполняемых функций персонала от имеющегося в нали­чии профессионального состава (экономистов, маркетологов, ин­женеров и т.п.) — структурного параметра СУ. Кроме структурных существуют геометрические и другие параметры.

В параметрическом методе параметры выступают одной из важ­нейших базовых характеристик как элементов СУ, так и в целом всей системы. Они отражают взаимосвязи элементов, состояния и тенденции их развития.

Разделы параметрического исследования:

1. Общие характеристики системы, характеризующие целенаправленность, надежность, адаптивность, самоуправляемость, системность.
2. Параметры структуры: количество уровней, количество компонентов по уровням, структура численности, мощностей, фондов, финансового портфеля, парка оборудования и т.д., портфеля продукции и т.д., организационная структура, количество основных связей, интенсивность связей, степень непрерывности.
3. Параметры процессов: продолжительность (длительность цикла и его фаз), интенсивность, скорость, результативность, эффективность.
4. Параметры среды и положение организации в среде: объемы рынка и доля предприятия на рынке, размеры кредиторской и дебиторской задолженности, степень приверженности потребителей продукции предприятия.
5. Параметры материальной базы: величина производственных мощностей, в т.ч. по отдельным видам оборудования и технологическим переходам, конкретные параметры оборудования (ремонтная сложность, ремонтопригодность), фондовооруженность, энерговооруженность, размер производственных запасов.
6. Параметры персонала: общая численность, в т. ч. по подразделениям, численность по переходам, численность по потокам, численность по профессиональным и квалификационным группам, численность по образовательному уровню, по демографическим признакам.
7. Параметры продукта: объем выпускаемого продукта в натуральном выражении по отдельным видам, номенклатурным или ассортиментным группам, параметры качества продукта: себестоимость продукта, цена, объем производства в стоимостном выражении.
8. Параметры экономической эффективности: производительность (многозначно: по валовой, чистой, реализованной и т.д.), рентабельность (продаж, капитала, издержек и т. д.), фондоотдача.

Качественные и количественные признаки СУ тесно взаимосвя­заны между собой. При исследовании СУ в основном используются:

• количественные абсолютные и относительные параметры (как частные случаи — показатели). Показатели в абсолютном исчислении используются для описания исследуемых объектов (численность ППП, количество подразделений, затраты на персонал и т.п.), а относительные показатели для характеристики, например, темпов роста продаж, прибыли, численности, производительности труда персонала и т.п.;
• качественные признаки, в описательном виде характеризующие то или иное свойство системы (способ воздействия на управляемый объект, метод оценки и т.п.);
• классификационные признаки (параметры), характеризующие те свойства системы, которые не могут принимать участие в оценке, но позволяют отнести изучаемый объект к определенному классу (список специальностей сотрудников, перечень марок ТСУ, типов ОСУ);
• порядковые (ранговые) параметры, позволяющие качественно отличать друг от друга изучаемые объекты, что выражается в присвоении им, например, баллов (оценка успеваемости, оценка выступления спортсмена), разрядов (у рабочих, спортсменов, чиновников), должностных рангов (инженер 3, 2 и 1-й категории, старший, ведущий и главный инженер).

Показатели СУ могут быть единичными, комплексными, интегральными и обобщенными.

Единичный показатель СУ — показатель, относящийся только к одному из свойств СУ. Например, единичными показателями являют­ся численность ППП, количество функций управления. Его разновид­ностью выступает относительный единичный показатель, представляю­щий собой отношение единичного показателя к нормативному (базо­вому), выражаемому в относительных единицах или процентах.

Нормативный (базовый) показатель — показатель, принятый за исходный (эталонный) при сравнительных оценках СУ. В качестве базовых принимаются, например, показатели прогрессивных СУ или конкурентов.

Базовые показатели могут быть также единичными, комплекс­ными, интегральными и обобщенными.

Комплексный показатель — показатель, относящийся к несколь­ким свойствам продукции. С помощью данного показателя можно в целом охарактеризовать подсистему, элемент СУ.

Разновидностью комплексного показателя, позволяющего с экономической точки зрения оценить совокупность свойств системы, может служить показатель, отражающий соотноше­ние суммарного полезного эффекта от эксплуатации СУ и суммарных затрат на ее создание и эксплуатацию, определяемый по формуле:


К комплексным показателям принадлежат также групповые и обобщенные (определяющие) показатели.

Комплексный показатель СУ, относящийся к определенной группе ее свойств, называется групповым.

Обобщенный показатель СУ— показатель, относящийся к такой сово­купности ее свойств, по которой принято решение оценивать систему.

Вся рассмотренная система показателей (рис. 21), как правило, используется для оценки СУ.


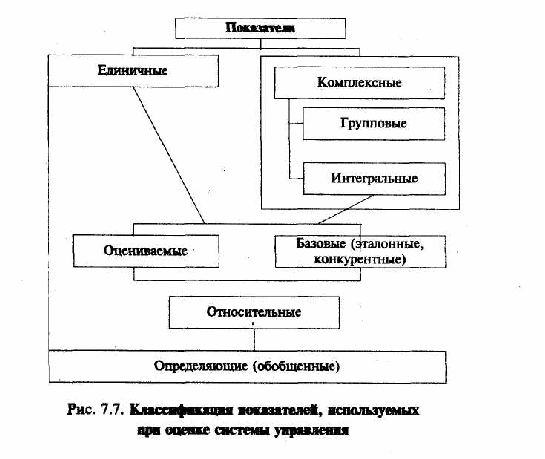
Рис. 21

В связи с тем, что каждая СУ может иметь бесчисленное множе­ство свойств, показателей, соответственно, может быть такое же множество. В зависимости от цели использования выбирают опре­деленное количество показателей, которыми и оперируют. Для об­легчения практического использования показателей проводят их классификацию.

Большое значение при этом имеет единство методов классифи­кации, определения и применения показателей.

Классификация показателей может быть произведена:

• по количеству характеризуемых свойств, т. е. они могут быть единичными и комплексными (групповыми, интегральными, обобщенными);
• по способу выражения (размерными и безразмерными единицами измерения, в том числе с помощью баллов, процентов);
• по методу определения (социологическими, экспертными, расчетными, экспериментальными);

• по влиянию на качество при изменении абсолютного значения показателя (позитивные, негативные);
• по видам ограничения (не менее, не более, не менее и не более);

Показатели с ограничениями, характеризуя определенное свойство СУ, при превышении допустимого численного значения превращают эффект в нуль. Поэтому на такие показатели при проведении оценки следует обращать особое внимание. Их можно назвать показателями вето на эффект. В большей части это относится к показателям назначения, надежности, безопасности и экологичности.

• по стадии определения — показатели исследовательско-проектные и эксплуатационные (показатели, определяемые при исследовании и проектировании, называют исследовательско-проектными, а формирующиеся в ходе функционирования систем — эксплуатационными);
• по применению для оценки (базовыми, относительными);
• по отношению к различным свойствам (адаптивности, эффективности, гибкости, преемственности и т.д.).

Особое значение для объективной оценки имеют те показатели, которые классифицированы по видам ограничений нормативно-технической документации (НТД) их чис­ленных значений (рис. 7.8). В некоторых случаях величины допус­тимых ограничений определяются специалистами исходя из усло­вий использования и соответствующих требований потребителей.

При поведении оценки необходимо оговорить (как в ручных, так и машинных расчетах), что для показате­лей с ограничениями должно соблюдаться условие следующих видов. 1. Для позитивных показателей:

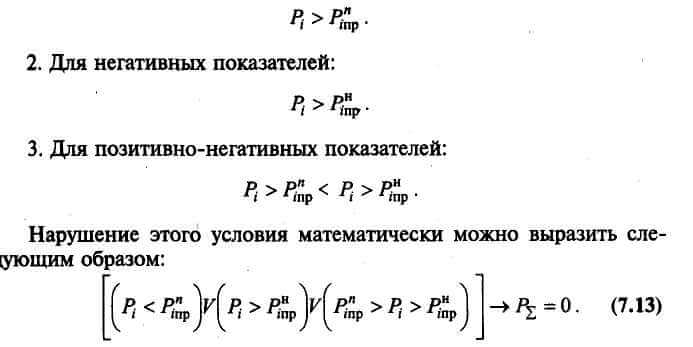
Рис. 7.8. Показатели системы управления, классифицированные по видам ограничения научно-технической документацией их численных значений

Показатели, имеющие ограничения

Неограниченные (некритические, т.е. не имеющие в НТД ограничений на изменение численных значений показателей)

Неограниченные позитивные (некритически позитивные, т.е. не имеющие в НТД ограничений на изменение численных значений показателей; при увеличении их численных значений эффект повышается)

Неограниченные негативные (некритически негативные, т.е. не имеющие в НТД ограничений на изменение численных значе­ний показателей; при увеличении их численных значений эффект снижается)

Ограниченные (критические, т.е. имеющие в НТД ограничения на изменение численных значений показателей)

Ограниченные позитивные (критически позитивные, т.е. имеющие в НТД ограничения на изменение численных значений показателей «снизу» и «не менее», для которых при увеличении их численного значения свойственно увеличение эффекта)

Ограниченные негативные (критически негативные, т.е. имею­щие в НТД ограничения на изменение численных значений показателей «снизу» и «не более», для которых при увеличении их численного значения свойственно уменьшение эффекта)

Ограниченные позитивно-негативные (критические позитивно-негативные, т.е. имеющие в НТД ограничения на изменение численных значений показателей от имеющегося номинального значения «снизу — сверху» и «не менее — не более», для которых при увеличении и уменьшении численного значения от номинального свойственно уменьшение эффекта)

Это означает, что при несоблюдении ограничений данный показатель равен нулю и уровень СУ также становится равным нулю. В большей части это относится к показателям назначения, надежности, безопасности и экологичности, так как значения их должны соответствовать требованиям стандартов или других НТД стран — потребителей данной продукции.

Объективная оценка СУ может быть дана только на основе системы взаимосвязанных параметров и показателей. При этом каждый показатель должен соответствовать требованиям:

• конкретизации и видоизменения в зависимости от целей оценки;
• развития и совершенствования объекта оценки;
• обеспечения единства количественных и качественных характеристик;
• адресности;
• сопоставимости;
• взаимосвязанности;
• простоты;
• информативности;
• достоверности и объективности.

Учитывая, что СУ предназначаются для дли­тельной эксплуатации, в качестве основных показателей надежно­сти системы, выпускающей продукцию первой категории, целесо­образно принять предельные вероятности исправной работы и от­каза. Эти вероятности могут быть выражены в качестве относительных долей времени, в течение которых система будет соответственно обеспечивать бесперебойное управление.

Общий порядок использования параметрического метода при исследовании объектов СУ предполагает следующие действия.

1. построить дерево свойств объекта исследования и его компо­нентов;
2. идентифицировать свойства свойств исследуемого объекта по классам;
3. определить номенклатуры параметров, характеризующих свойства исследуемого объекта СУ;
4. осуществить группировку избранных параметров;
5. провести шкалирование (по типам шкал: порядковая; интервалов; отношений; разностей; абсолютная) параметров;
6. осуществить нормирование значений параметров;
7. измерить значения параметров;
8. разработать модели взаимного соответствия сопоставляемых компонентов и параметров объекта (рис. 22);
9. рассчитать обобщенные оценки состояния объекта и его компонентов.

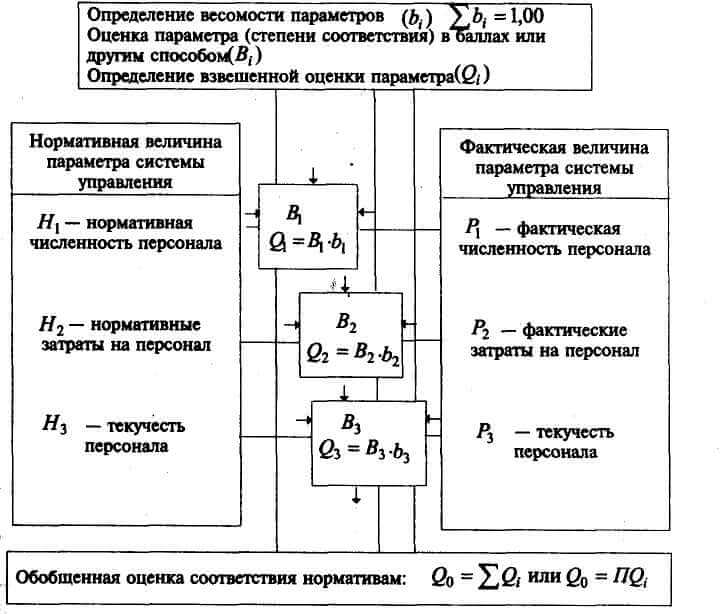
Рис. 22. Модель параметрического взаимного соответствия параметров системы управления

СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ

В статистическом анализе производится обра­ботка некоторой случайной выборки, под которой понимают­ся результаты N последовательных и независимых экспери­ментов со случайной величиной или событием. Выборка должна обеспечивать репрезентативность исследования. Объем обрабатываемой информации должен быть достаточен для полу­чения результатов с требуемой точностью и надежностью.

Используется для исследования про­цессов и объектов на основе массовых данных, полученных из статистической или учетной документации, по результатам разного рода обследований и экспериментов.

Статистический анализ может использоваться для изучения как внутренней, так и внешней среды. При изучении внутренней среды наибольшее значение имеет исследование: влияния различных факторов на формирование прибыли (формирование экономических показателей за счет влияния совокупности значимых факторов): формирования и развития персонала организации; формирования и развития потенциала организации; качества продукции и т. д.

В рамках изучения внешней среды большое значение имеет статистический анализ состояния рынка, анализ дифференциации спроса, оценка потребителей (их платежеспособности), конкурентов, поставщиков, деловых партнеров.

Наиболее употребительными методами статистического анализа систем управления являются: регрессионный анализ; корреляционный анализ; дисперсионный анализ; анализ временных рядов; факторный анализ.

Регрессионный анализ

Регрессионный анализ ставит своей задачей исследование зависимости одной случайной величины от ряда других слу­чайных и неслучайных величин (регрессия — зависимость ма­тематического ожидания случайной величины от значений других случайных величин). Например, после проведения N экспериментов на статистической модели получен набор реа­лизаций случайных величин {X_i Y_i,}, i = 1, 2, 3, …, п , где X яв­ляется независимой переменной, а Y — функцией. Обработка этого массива случайных величин позволяет их представить в виде детерминированной линейной регрессивной модели типа:

Y= a₀ + a₁ X, (3.1)

где a₁ – коэффициент регрессии, среднее число единиц на которое увеличится или уменьшится результативный признак при изменении значения фактора на одну единицу;
a₀ – минимальное значение результативного признака при нулевом значении фактора.

(3.2)

где x_j⁽⁰⁾ являются «базовыми» значениями всех k перемен­ных, в окрестностях которых анализируется характер иссле­дуемого процесса.

Выражение (3.3) представляет собой линейную функцию, однако, если значения Δх_j,- достаточно велики или функция Y существенно нелинейна, то можно использовать разложение более высокого порядка.

При анализе регрессионной модели (3.3) значения коэффи­циентов a_j показывают степень влияния j-й переменной на функцию Y, что позволяет разделить все переменные на «суще­ственные» и «несущественные». Наибольший интерес регрессионная модель представляет для прогноза поведения функций Y. В практической деятельности регрессионный ана­лиз часто используется для создания так называемой эмпириче­ской модели, когда, обрабатывая результаты наблюдений (или характеристики существующих систем), получают регрессион­ную модель и используют ее для оценки перспективных систем или поведения системы при гипотетических условиях.

Точность и надежность получаемых оценок зависят от чис­ла наблюдений и расположения прогностических значений х_j относительно базовых (т.е. из­вестных на некоторый момент времени) х_j⁽⁰⁾ Чем больше раз­ность Δх_j, тем меньше точность прогноза.

Корреляционный анализ

Корреляционный метод — один из экономико-математических методов исследования, позволяющий определить количественную взаимосвязь между несколькими явлениями исследуемой системы. Он используется для определения сте­пени взаимосвязи между случайными величинами (корреляция — зависимость между случайными величинами, выражающая тенденцию одной величины возрастать или убы­вать при возрастании или убывании другой).

Корреляционная зависимость в отличие от функциональной может проявляться только в общем, среднем случае, т.е. в массе случаев — наблюдений. Поэтому корреляция представляет собой вероятностную зависимость между явлениями, при которой средняя величина параметров одного из них изменяется в зависимости от других. Корреляция между двумя явлениями носит название парной, а между несколькими — множественной.

При использовании корреляционного метода выделяют функ­цию, т.е. исследуемый результирующий показатель и факторные признаки, от которых зависит результирующий, — аргументы. Та­кая классификация проводится на основе качественного анализа, т.е. все возможные переменные подразделяют на зависимые и неза­висимые от изучаемого явления.

Корреляционные связи в зависимых переменных не могут быть жесткими и носят характер неполных связей. Если в случае увели­чении (или уменьшении) аргумента результирующий показатель (функция) также увеличивается (или соответственно уменьшается), то корреляционная связь называется прямой (положительной), а если наоборот — обратной (отрицательной). При отсутствии какой-либо зависимости функции от аргумента, корреляционная связь отсутствует.

Теснота корреляционной взаимосвязи при линейной зависимо­сти оценивается коэффициентами корреляции, при нелинейной за­висимости — корреляционным отношением.

Корреляционной характеристикой является коэффициент корреляции, равный математическому ожиданию произведе­ний отклонений случайных величин x_i и х_j от своих математи­ческих ожиданий и нормированный относительно среднеквадратических отклонений данных случайных величин.

Если число случайных величин больше двух (r > 2), то со­ставляется квадратная корреляционная матрица размером (r x r), элементами которой является коэффициенты корреляции k_ij , a диагональные элементы равны единице (т.е. k_ij =1). Коэффици­енты корреляции изменяется от нуля до единицы, и чем больше его значение, тем теснее связь между случайными величинами.

Оценка коэффициентов корреляции рассчитываются по значениям оценок математических ожиданий и среднеквадратических отклонений, полученных путем статистической об­работки результатов реализаций случайных величин.

Следует отметить, что коэффициент корреляции может коле­баться в пределах от 1 до 0 и от 0 до + 1. Чем ближе рассчитываемый коэффициент корреляции к +1 (при прямой зависимости) и к -1 (при обратной зависимости), тем выше теснота связи. Соответ­ственно при коэффициентах корреляции +1 или —1 имеют место функциональные связи.

Важнейшая задача корреляционного метода — определение вида корреляционного уравнения (уравнения регрес­сии).

Простейшим видом такого уравнения, характеризующим взаи­мосвязь между двумя параметрами, может быть уравнение прямой (рис. 7.1):

Y= a + bX, (7.1)

где X, Y— соответственно независимая и зависимая переменные;

а, b — постоянные коэффициенты (а определяет начало отсчета, b — угол наклона прямой).

Примером однофакторной нелинейной зависимости может быть также формула другого вида, например при наличии степенной за­висимости:

Вывод о прямолинейном характере зависимости можно прове­рить путем простого сопоставления имеющихся данных или графи­ческим способом (регистрацией в прямоугольной системе координат значений У и X, расположение которых на графике позволяет сделать вывод о правильности или ошибочности представления о линейном характере зависимости между двумя изучаемыми параметрами).

Другая задача метода корреляционного анализа — определе­ние постоянных коэффициентов связи между переменными пара­метрами, которые наилучшим образом будут отвечать имею­щимся фактическим значениям Y и X.

В данном случае в качестве критерия оценки адекватности линейной зависимости фактическим данным можно исполь­зовать минимум суммы квадратов отклонений реальных ста­тистических значений Y от рас­считанных по уравнению при­нятой к применению прямой.

Дисперсионный анализ

Дисперсионный анализ используется для проверки стати­стических гипотез о влиянии на показатели качественных факторов, т.е. факторов, не поддающихся количественному измерению (например, качественный фактор — организация производства, влияющий на количественный показатель — прибыль от производства). В этом заключается его отличие от регрессионного анализа, в котором факторы выступают как параметры, имеющие количественную меру (например, коли­чественный фактор — затраты на производство).

В дисперсионном анализе качественный фактор представляется j-ми возможностями состояниями (например, возможными схемами организации производства), для оценки которых по каждому из них проводится n_j экспериментов.

Далее рассчитываются статистические оценки в каждой n_j группе экспериментов и в общей выборке N, а затем анализируется соотношение между ними. По этому соотноше­нию принимается или отвергается гипотеза о влиянии качест­венного фактора на показатель.

Метод временных рядов

Анализ временных рядов используется при исследовании дискретного случайного процесса, протекающего на интерва­ле времени Т .

Результаты экспериментов или наблюдений, полученные на данном интервале, представляются в виде временного ряда, каждое значение Y_i которого включает детерминированную f(t) и случайную z(t) составляющие:

Детерминированная составляющая описывает влияние де­терминированных факторов в момент времени t, влияние же множества случайных факторов описывает случайная состав­ляющая. Детерминированную часть временного ряда называ­ют трендом. Этот временной ряд описывается трендовой моделью:

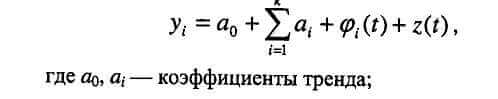
k — количество функций времени, линейная комбинация

которых определяет детерминированную составляющую (i от 1 до k);

φ_i (t) — функция времени.

В процессе анализа вид функции времени φ_i(t)<0 постулируется исследователем в виде рабочей гипотезы. Это может быть степенная функция tⁿ, либо тригонометрическая. Коэффициенты тренда и оценку дисперсии случай­ной составляющей определяют путем проведения статистиче­ской обработки результатов эксперимента или наблюдений.

С помощью представления случайного процесса в виде временных рядов можно, во-первых, исследовать динамику этого процесса, во-вторых, выделить факторы, существенным образом влияющие на показатели, и определить периодич­ность их максимального воздействия, в-третьих, провести ин­тервальный или точечный прогноз показателя Y на некоторый промежуток времени Δt (точечный прогноз указывает лишь точку, возле которой может находиться прогнозируемый по­казатель, интервальный — интервал нахождения этого показа­теля с некоторой заданной вероятностью).

Факторный анализ

Для того чтобы обеспечить эффективное функционирование организации необходимо при принятии управленческих решений учитывать все существенные факторы, влияющие на функционирование и развитие предприятия, как внешние (влияющие на уровне макросреды и контактной среды), так и внутренние.

Факторный анализ является частью многомерного статистиче­ского анализа, входящего в математико-статистические методы. Сущность метода факторного анализа заключается в выделении из множества изучаемых факторов, влияющих на изучаемый объект, наиболее значимых.

Фактор представляет собой обычно независимую переменную, нередко называемую причиной, и находящуюся в логической зависимости со следствием изучаемого явления и определяющую его величину.

Например, используемая компьютерная техника и ее программное обеспечение выступают существенным фактором произ­водительности труда работников управления (бухгалтеров, менеджеров, экономистов и др.); изменяющиеся факторы трудовых затрат и производительности труда влияют на изменение объемов выпуска продукции.

Фактор может быть единичным, т.е. влияющим на следствие од­ной переменной, или комплексным, т.е. влияющий одновременно на несколько переменных. Комплексный фактор, связанный со всеми переменными, называют генеральным.

В отличие от корреляционного анализа рассматриваемый метод не требует подразделять все переменные на зависимые и независимые, так как в нем все переменные величины (факторы — причины), опре­деляющие явление, рассматриваются как равноправные. При этом следует учитывать, что некоторые из переменных величин могут быть в некоторый период времени стабильными, т.е. не изменяющимися.

Например, прирост объемов выпуска продукции при неиз­менности числа работающих в анализируемые периоды времени и при повышающейся производительности труда есть следствие изме­нения только одного фактора — производительности труда.

Описание влияния факторов на деятельность организации имеет высокую сложность, поскольку действие многих факторов имеет латентный (скрытый) характер.

Отбор факторов, влияющих на исследуемый объект, осуществ­ляется, как правило, на основе их классификации, теоретического обоснования и путем их качественного анализа. При этом необхо­димо учитывать взаимодействие факторов между собой. Число фак­торов должно быть ограниченным необходимым минимумом. От маловажных факторов нужно абстрагироваться.

Для каждого выбранного фактора следует предусматривать возможность его количественной оценки, так как она потребуется в дальнейшем при определении корреляционных зависи­мостей между ними и оценки влияния их на объект исследования.

Метод факторного анализа широко используется при анализе влияния различных факторов (труда, использования оборудования, использования производственных мощностей в целом, использова­ния сырья и материалов, организации производства, технологии и др.) на объемы производства, качество выпускаемой продукции, фонд заработной платы, итоги хозяйственной деятельности и раз­витие предприятия в целом.