- Есть вопросы?
- 8(961)1155384
- zakaz@kursach37.com
Пример решения задач по Эконометрике

ТЕМА 1. ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ (ДЕ 1 )
Задание 1
Решение: Расположим выборку по возрастанию фактора Х.
Тогда матрица расчета коэффициента корреляции будет выглядеть следующим образом.
Таблица 1.1 – Изучение зависимости У1 от Х при помощи коэффициента корреляции
|
|
y1 |
x1 |
x2 |
x3 |
х4 |
x5 |
x6 |
| y1 |
1 |
||||||
| x1 |
0,900007 |
1 |
|||||
| x2 |
-0,12087 |
0,150682 |
1 |
||||
| x3 |
0,037188 |
0,312059 |
0,901025 |
1 |
|||
| х4 |
0,304637 |
0,518792 |
0,830058 |
0,855538 |
1 |
||
| x5 |
0,304682 |
0,5342 |
0,881956 |
0,873584 |
0,976141 |
1 |
|
| x6 |
0,495082 |
0,709812 |
-0,00649 |
0,075977 |
0,196458 |
0,230714 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х1 (выделено желтым цветом).
Таблица 1.2 – Изучение зависимости У2 от Х при помощи коэффициента корреляции
|
|
y2 |
x1 |
x2 |
x3 |
х4 |
x5 |
x6 |
| y2 |
1 |
||||||
| x1 |
0,180518 |
1 |
|||||
| x2 |
0,708067 |
0,150682 |
1 |
||||
| x3 |
0,409461 |
0,312059 |
0,901025 |
1 |
|||
| х4 |
0,651681 |
0,518792 |
0,830058 |
0,855538 |
1 |
||
| x5 |
0,713489 |
0,5342 |
0,881956 |
0,873584 |
0,976141 |
1 |
|
| x6 |
0,127507 |
0,709812 |
-0,00649 |
0,075977 |
0,196458 |
0,230714 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х2 и Х5.
Таблица 1.3 – Изучение зависимости У4 от Х при помощи коэффициента корреляции
|
|
y4 |
x1 |
x2 |
x3 |
х4 |
x5 |
x6 |
| y4 |
1 |
||||||
| x1 |
0,570025 |
1 |
|||||
| x2 |
0,820432 |
0,150682 |
1 |
||||
| x3 |
0,863177 |
0,312059 |
0,901025 |
1 |
|||
| х4 |
0,995525 |
0,518792 |
0,830058 |
0,855538 |
1 |
||
| x5 |
0,975715 |
0,5342 |
0,881956 |
0,873584 |
0,976141 |
1 |
|
| x6 |
0,236648 |
0,709812 |
-0,00649 |
0,075977 |
0,196458 |
0,230714 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х2, Х3, Х4 и Х5.
Таблица 1.4 – Изучение зависимости У5 от Х при помощи коэффициента корреляции
|
y5 |
x1 |
x2 |
x3 |
х4 |
x5 |
x6 |
|
| y5 |
1 |
||||||
| x1 |
0,518792 |
1 |
|||||
| x2 |
0,830058 |
0,150682 |
1 |
||||
| x3 |
0,855538 |
0,312059 |
0,901025 |
1 |
|||
| х4 |
1 |
0,518792 |
0,830058 |
0,855538 |
1 |
||
| x5 |
0,976141 |
0,5342 |
0,881956 |
0,873584 |
0,976141 |
1 |
|
| x6 |
0,196458 |
0,709812 |
-0,00649 |
0,075977 |
0,196458 |
0,230714 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х2, Х3, Х5. (по условию задачи Х4 = У5, поэтому коэффициент равен 1.)
Таблица 1.5 – Изучение зависимости У6 от Х при помощи коэффициента корреляции
|
|
y6 |
x1 |
x2 |
x3 |
х4 |
x5 |
x6 |
| y6 |
1 |
||||||
| x1 |
0,751978 |
1 |
|||||
| x2 |
-0,15202 |
0,150682 |
1 |
||||
| x3 |
-0,04321 |
0,312059 |
0,901025 |
1 |
|||
| х4 |
0,099107 |
0,518792 |
0,830058 |
0,855538 |
1 |
||
| x5 |
0,135123 |
0,5342 |
0,881956 |
0,873584 |
0,976141 |
1 |
|
| x6 |
0,979567 |
0,709812 |
-0,00649 |
0,075977 |
0,196458 |
0,230714 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х1 и Х6.
Таблица 1.6 – Изучение зависимости У7 от Х при помощи коэффициента корреляции
|
|
У7 |
Х7 |
Х8 |
Х9 |
| У7 |
1 |
|||
| Х7 |
0,9216397 |
1 |
||
| Х8 |
0,73928832 |
0,77550633 |
1 |
|
| Х9 |
0,83139675 |
0,83349394 |
0,93757122 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х7, Х8, Х9.
Таблица 1.7 – Изучение зависимости У8 от Х при помощи коэффициента корреляции
|
|
У8 |
Х7 |
Х8 |
Х9 |
| У8 |
1 |
|||
| Х7 |
0,599705 |
1 |
||
| Х8 |
0,871722 |
0,775506 |
1 |
|
| Х9 |
0,735168 |
0,833494 |
0,937571 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х8, Х9.
Таблица 1.8 – Изучение зависимости У9 от Х при помощи коэффициента корреляции
|
|
У9 |
Х7 |
Х8 |
Х9 |
|
У9 |
1 |
|||
|
Х7 |
0,760096 |
1 |
||
|
Х8 |
0,887626 |
0,775506 |
1 |
|
|
Х9 |
0,985119 |
0,833494 |
0,937571 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х7, Х8, Х9.
Таблица 1.9 – Изучение зависимости У10 от Х при помощи коэффициента корреляции
|
|
У10 |
Х7 |
Х8 |
Х9 |
|
У10 |
1 |
|||
|
Х7 |
0,864063 |
1 |
||
|
Х8 |
0,97702 |
0,775506 |
1 |
|
|
Х9 |
0,978537 |
0,833494 |
0,937571 |
1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, имеет сильную прямую связь с фактором Х7, Х8, Х9.
Приведем интерпретацию некоторых из коэффициентов и зависимостей:
Rх1у1 = 0.900, прямая сильная линейная связь свидетельствует о том, что чем выше среднемесячная заработная плата работающих , тем выше уровень среднедушевых денежных расходов за месяц.
Rх2у2 = 0.70, прямая сильная линейная связь свидетельствует о том, что чем выше сальдированный финансовый результат (прибыль) за год, тем выше уровень инвестиции в основной капитал предприятий.
Rх3у2 =0.4, прямая умеренная линейная связь свидетельствует о том, что чем выше сальдированный финансовый результат (прибыль) за год, тем выше уровень инвестиции в основной капитал предприятий в предыдущем году.
Rх4у4 =0.99, прямая сильная линейная связь свидетельствует о том, что чем выше доходы консолидированных бюджетов, тем выше размер их консолидированных расходов.
Rх5у5 = 0.976, прямая сильная линейная связь свидетельствует о том, что чем выше уровень валового регионального продукта, тем выше размер консолидированных доходов бюджета.
Rх6у6 =0.979 прямая сильная линейная связь свидетельствует о том, что чем выше среднегодовая численность экономически активнго населения, тем выше оборот розничной торговли за год.
Rх7у7 = 0.92, прямая сильная линейная связь свидетельствует о том, что чем выше размер среднемесячной начисленной заработной платы, тем выше уровень среднедушевых расходов в месяц.
Rх8у8 = 0.871, прямая сильная линейная связь свидетельствует о том, что чем выше сальдированный финансовый результат, тем выше размер инвестиций в основной капитал предприятий.
Rх9у9 = 0.985, прямая сильная линейная связь свидетельствует о том, что чем больше поступлений в пенсионный фонд, тем выше уровень расходов данного фонда.
Rх9у10 = 0.978, прямая сильная линейная связь свидетельствует о том, что чем выше уровень валового регионального продукта, тем выше уровень поступлений в пенсионный фонд.
3) Рассчитать параметры a0, a1 уравнения парной регрессии y = a0 + a1x . Дать характеристику полученным результатам.
Воспользуемся исходными данными для расчета параметров уравнения парной регрессии.
Таблица 1.10 – Расчет коэффициентов для уравнения регрессии.
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
| Y-пересечение |
0,205166 |
1,626715 |
0,126123 |
0,91117 |
-6,79403 |
7,204356 |
| Переменная X 1 |
0,808954 |
0,342356 |
2,362906 |
0,141942 |
-0,66408 |
2,281992 |
| Переменная X 2 |
-0,03592 |
0,057343 |
-0,62637 |
0,595035 |
-0,28265 |
0,210811 |
| Переменная X 3 |
-0,02041 |
0,045619 |
-0,44744 |
0,698349 |
-0,2167 |
0,175872 |
| Переменная X 4 |
-0,08977 |
0,247027 |
-0,36341 |
0,751119 |
-1,15264 |
0,973102 |
| Переменная X 5 |
0,026995 |
0,051463 |
0,524554 |
0,652236 |
-0,19443 |
0,248424 |
| Переменная X 6 |
-0,75198 |
0,498535 |
-1,50838 |
0,270488 |
-2,89701 |
1,393042 |
Тогда уравнение регрессии примет вид (показатели у1 и х1 – 6)
![]()
Аналогично рассчитаем для (У2 и х1 – 6)
Таблица 1.11 – Расчет коэффициентов для уравнения регрессии
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95,0% |
| Y-пересечение |
7,62733 |
16,04273 |
0,475439 |
0,68134 |
-61,3989 |
76,65361 |
| Переменная X 1 |
-4,0597 |
3,376325 |
-1,2024 |
0,352251 |
-18,5869 |
10,46745 |
| Переменная X 2 |
0,821038 |
0,565523 |
1,451821 |
0,283676 |
-1,61221 |
3,254285 |
| Переменная X 3 |
-2,3239 |
0,449899 |
-5,16537 |
0,035496 |
-4,25966 |
-0,38814 |
| Переменная X 4 |
-0,93626 |
2,436192 |
-0,38431 |
0,737762 |
-11,4183 |
9,545833 |
| Переменная X 5 |
0,867034 |
0,507534 |
1,708328 |
0,2297 |
-1,31671 |
3,050776 |
| Переменная X 6 |
5,138908 |
4,916575 |
1,045221 |
0,405634 |
-16,0154 |
26,29322 |
![]()
Аналогично рассчитаем для (У3 и х1 – 6)
Таблица 1.12 – Расчет коэффициентов для уравнения регрессии
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95,0% |
| Y-пересечение |
-1,15145 |
1,260761 |
-0,91329 |
0,457497 |
-6,57606 |
4,273172 |
| Переменная X 1 |
0,466284 |
0,265338 |
1,757322 |
0,220942 |
-0,67537 |
1,60794 |
| Переменная X 2 |
0,040441 |
0,044443 |
0,909946 |
0,458902 |
-0,15078 |
0,231664 |
| Переменная X 3 |
0,017865 |
0,035357 |
0,505272 |
0,663548 |
-0,13426 |
0,169992 |
| Переменная X 4 |
1,010335 |
0,191455 |
5,277145 |
0,034084 |
0,186571 |
1,834098 |
| Переменная X 5 |
-0,03625 |
0,039886 |
-0,90883 |
0,459374 |
-0,20786 |
0,135366 |
| Переменная X 6 |
-0,16684 |
0,386382 |
-0,4318 |
0,707983 |
-1,82931 |
1,495631 |
![]()
Задача 2
По территориям Северо-Западного федерального округа РФ приводятся данные за 2004 г. Выявить и оценить зависимость сальдированного финансового результата (прибыли) за год, млрд руб., (y2) от инвестиций в основной капитал в 2004 г., млрд руб., x2 ![]()
Решение:
На основе исходных табличных данных выполним расчет коэффициентов корреляции и регрессии.
Таблица 2.1 – Исходные данные задачи
| Территории федерального округа |
Сальдированный финансовый результат (прибыль) за год, млрд руб., y2 |
Инвестиции в основной капитал в 2004 г., млрд. руб., |
| Республика Карелия |
2,21 |
12,60 |
| Республика Коми |
17,45 |
30,20 |
| Архангельская обл. |
8,60 |
30,50 |
| Вологодская обл. |
61,05 |
41,45 |
| Калининградская обл. |
5,76 |
18,11 |
| Ленинградская обл. |
33,38 |
67,02 |
| Мурманская обл. |
16,22 |
13,53 |
| Новгородская обл. |
3,88 |
7,95 |
| Псковская обл. |
0,75 |
5,75 |
Тогда имеем исходную таблицу данных:
Таблица 2.2– Исходные параметры У и Х
| У2 | Х2 |
|
2,21 |
12,60 |
|
17,45 |
30,20 |
|
8,60 |
30,50 |
|
61,05 |
41,45 |
|
5,76 |
18,11 |
|
33,38 |
67,02 |
|
16,22 |
13,53 |
|
3,88 |
7,95 |
|
0,75 |
5,75 |
Выполним построение корреляционного поля, тогда получим.
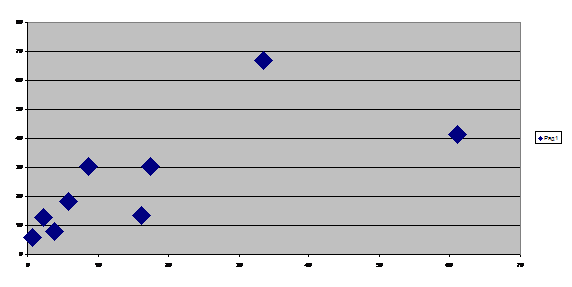
Рисунок 1 — Корреляционное поле.
Анализ корреляционного поля данных показывает, что между признаками ![]() и
и ![]() в выборочной совокупности существует прямая и достаточно тесная связь. Коэффициент парной корреляции составил Rх2у2 = 0,708, это значит, что связь прямая сильная, то есть чем выше уровень прибыли, тем выше объем инвестиций в основной капитал. Тогда, объясняемая переменная
в выборочной совокупности существует прямая и достаточно тесная связь. Коэффициент парной корреляции составил Rх2у2 = 0,708, это значит, что связь прямая сильная, то есть чем выше уровень прибыли, тем выше объем инвестиций в основной капитал. Тогда, объясняемая переменная ![]() линейно зависит от фактора
линейно зависит от фактора ![]() , поэтому уравнение регрессии будем искать в виде
, поэтому уравнение регрессии будем искать в виде ![]() ,.
,.
Найдем коэффициенты для уравнения регрессии.
Выполним оценку регрессии.
Таблица 2.3 – Коэффициенты уравнения регрессии
|
|
Коэффициенты |
| Y-пересечение |
-1,19961 |
| Переменная X 1 |
0,704929 |
На основании этих данных запишем уравнение регрессии:
![]()
Коэффициент а называется выборочным коэффициентом регрессии ![]() Коэффициент регрессии
Коэффициент регрессии ![]() показывает, на сколько единиц в среднем изменяется переменная
показывает, на сколько единиц в среднем изменяется переменная ![]() при увеличении переменной
при увеличении переменной ![]() на одну единицу.
на одну единицу.
4) Оценить точность а0, а1 с помощью t- статистики с уровнем значимости a=0,05
Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации.
Таблица 2.4 – Индекс детерминации
| Регрессионная статистика | |
| R-квадрат | 0,501359 |
![]() .
.
Значение детерминации R-квадрат имеет значение, чуть больше 50%.
Параметр R-квадрат, представляет собой квадрат коэффициента корреляции rxy2 и называется коэффициентом детерминации. Величина данного коэффициента характеризует долю дисперсии зависимой переменной y, объясненную регрессией (объясняющей переменной x). Соответственно величина 1 — rxy2 характеризует долю дисперсии переменной y, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет: 0,501, или 50,1%.
Находим, что численное значение ![]() , а скорректированный (нормированный, исправленный) коэффициент детерминации равен
, а скорректированный (нормированный, исправленный) коэффициент детерминации равен ![]()
1) Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации ![]() : проверяется нулевая гипотеза
: проверяется нулевая гипотеза ![]() , используется
, используется ![]() .
.
Наблюдаемое значение критерия ![]() и оценку его значимости находим в следующей таблице 2.5.
и оценку его значимости находим в следующей таблице 2.5.
Таблица 2.5 — Дисперсионный анализ
| F |
Значимость F |
|
7,038151 |
0,032801 |
Включаемые в уравнение множественной регрессии факторы должны объяснить вариацию зависимой переменной. Если строится модель с некоторым набором факторов, то для нее рассчитывается показатель детерминации, который фиксирует долю объясненной вариации результативного признака (объясняемой переменной) за счет рассматриваемых в регрессии факторов. А оценка влияния других, неучтенных в модели факторов, оценивается вычитанием из единицы коэффициента детерминации, что и приводит к соответствующей остаточной дисперсии.
Таким образом, при дополнительном включении в регрессию еще одного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит и данные показатели практически недостаточно значимо отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и практически является лишним фактором.
Если модель насыщается такими лишними факторами, то не только не снижается величина остаточной дисперсии и не увеличивается показатель детерминации, но, более того, снижается статистическая значимость параметров регрессии по критерию Стьюдента вплоть до статистической незначимости.
2) Для статистической оценки значимости коэффициентов регрессии (а0, а1) используем ![]() статистику Стьюдента.
статистику Стьюдента.
Проверяется нулевая гипотеза ![]() .
.
Для проверки нулевой гипотезы необходимо знать величину наблюдаемых значений критерия ta0 и ta1. Их значения и оценки их статистической значимости найдем в таблице 2.6.
Таблица 2.6 – Параметры t — статистики
| t-статистика | P-Значение |
|
-0,14423 |
0,889383 |
|
2,652951 |
0,032801 |
В таблице 2.7 находим границы доверительных интервалов для каждого из параметров:
Таблица 2.7 – Границы доверительных интервалов
| Нижние 95% | Верхние 95% |
|
-20,8669 |
18,46772 |
|
0,076613 |
1,333245 |
Табличное значение критерия Стьюдента составило t = 2,12, тогда
tа0 = 0,14
tа1 = 2,65
Значимым является Та1, так как 2,65 > 2.11.
5) Оценить надёжность уравнения с помощью индекса детерминации R2 и F – критерия Фишерадля уровня значимости a = 0,05.
По данным регрессионного анализа можно сказать:
— т.к. коэффициент детерминации равен 0,7, то вариация результата на 70% объясняется вариацией факторов.
— F-критерий равен 7,03, его табличное значение 4, 26. т.к. фактическое значение превышает табличное, то делаем вывод, что полученной уравнение регрессии статистически значимо.
6) Рассчитайте прогнозное значение результата![]() , если прогнозное значение фактора (
, если прогнозное значение фактора (![]() ) составит 1,062 от среднего уровня (
) составит 1,062 от среднего уровня (![]() ).
).
7) Рассчитайте интегральную и предельную ошибки прогноза (для
a = 0,05), определите доверительный интервал прогноза (![]() ;
; ![]() ), оценив таким образом точность выполненного прогноза.
), оценив таким образом точность выполненного прогноза.
Далее вычисляем прогнозные значения факторов:
Рассчитаем прогнозное значение результата![]() , если
, если
![]()
Х1 = ср.х * 1, 062 = 25,2 * 1,062 = 26,8
Затем, подставив эти значения в уравнение регрессии, получим прогнозное (предсказанное) значение фактора.
Упрогн = -1,19 + 0,704 * 26,8 = 18,86 -1.19 = 17,67
Доверительный интервал прогноза оценивается формулой: ![]() , где
, где ![]() — ошибка прогноза равна
— ошибка прогноза равна ![]() стандартная ошибка регрессии.
стандартная ошибка регрессии.
Таблица 2.8 – Параметры ошибки прогноза
| Стандартная ошибка | 14,76366 |
S = 14, 76, тогда
1) нижняя граница прогноза ![]() = 2,9 ,
= 2,9 ,
2) верхнюю границу прогноза ![]() = 32,433.
= 32,433.
Интервал прогнозных значений результативного признака
![]() =>
=>![]()
Ответ: Прогнозное значение результата![]() , если прогнозное значение фактора (
, если прогнозное значение фактора (![]() ) составит 1,062 от среднего уровня (
) составит 1,062 от среднего уровня (![]() ), указано в интервале:
), указано в интервале:
![]() .
.



