- Есть вопросы?
- 8(961)1155384
- zakaz@kursach37.com
Применение Excel в математических методах

Работа с матрицами. Балансовые модели
Задание. Межотраслевой баланс производства и распределения продукции для 4 отраслей имеет вид:
| Производящие отрасли |
Потребляющие отрасли |
Валовой продукт (Х) |
|||
|
1 |
2 |
3 |
4 |
||
|
1 |
80 |
45 |
85 |
95 |
475 |
|
2 |
25 |
35 |
20 |
30 |
825 |
|
3 |
15 |
15 |
55 |
75 |
650 |
|
4 |
95 |
5 |
5 |
95 |
820 |
1. Найти конечный продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат.
2. Какой будет конечный продукт каждой отрасли, если валовой продукт первой отрасли увеличится в 2 раза, у второй увеличится на половину, у третьей не изменится, у четвертой – уменьшится на 10 процентов.
3. Найти валовой продукт, если конечный станет равен 700, 500, 850 и 700.
Решение:
1. Составим матрицу коэффициентов прямых затрат А={aij}, где ![]() , j=1,2,…,n.
, j=1,2,…,n.
Зная величины валовой продукции (Xi) для каждой отрасли, можно определить объёмы конечной продукции каждой отрасли (Yi) по формуле:
Y = (E – A)X.
Для нахождения Y будем использовать функцию MS Excel, выполняющую умножение матриц «МУМНОЖ».
Чистую продукцию каждой отрасли (Zj) найдем по формуле:
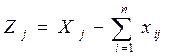
Таблица 1.1
Полная балансовая таблица для четырех отраслей, полученная на основе исходных данных
| Производящие отрасли |
Потребляющие отрасли |
Конечный продукт (Y) |
Валовой продукт (Х) |
|||
|
1 |
2 |
3 |
4 |
|||
|
1 |
80 |
45 |
85 |
95 |
170 |
475 |
|
2 |
25 |
35 |
20 |
30 |
715 |
825 |
|
3 |
15 |
15 |
55 |
75 |
490 |
650 |
|
4 |
95 |
5 |
5 |
95 |
620 |
820 |
|
Чистая продукция (Z) |
260 |
725 |
485 |
525 |
||
|
Валовой продукт (Х) |
475 |
825 |
650 |
820 |
||
Проверка: ![]()
![]()
2. Определим, какой будет конечный продукт каждой отрасли, если валовой продукт первой отрасли увеличится в 2 раза, у второй увеличится на половину, у третьей не изменится, у четвертой – уменьшится на 10 процентов, т.е. если 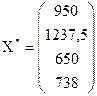 :
:
![]()
Рассчитаем дополнительно величину чистой продукции по каждой отрасли и запишем полную балансовую таблицу, соответствующую данной ситуации.
Таблица 1.2
| Производящие отрасли |
Потребляющие отрасли |
Конечный продукт (Y) |
Валовой продукт (Х) |
|||
|
1 |
2 |
3 |
4 |
|||
|
1 |
80 |
45 |
85 |
95 |
645 |
950 |
|
2 |
25 |
35 |
20 |
30 |
1127,5 |
1237,5 |
|
3 |
15 |
15 |
55 |
75 |
490 |
650 |
|
4 |
95 |
5 |
5 |
95 |
538 |
738 |
|
Чистая продукция (Z) |
735 |
1137,5 |
485 |
443 |
||
|
Валовой продукт (Х) |
950 |
1237,5 |
650 |
738 |
||
Проверка: ![]() .
.
3. Найдем валовой продукт, если конечный станет равен 700, 500, 850 и 700, т.е. 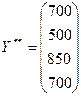 Для этого используем формулу:
Для этого используем формулу:
![]() ,
,
где ![]() — матрица коэффициентов полных материальных затрат.
— матрица коэффициентов полных материальных затрат.
На основе матрицы (Е-А) рассчитаем матрицу ![]() , используя функцию «МОБР» MS Excel.
, используя функцию «МОБР» MS Excel.
После расчета вектора валового продукта ![]() , элементы хij (объём продукции отрасли i, расходуемой в отрасли j) рассчитаем по формуле:
, элементы хij (объём продукции отрасли i, расходуемой в отрасли j) рассчитаем по формуле:
![]() .
.
Рассчитаем дополнительно величину чистой продукции по каждой отрасли и запишем полную балансовую таблицу, соответствующую данной ситуации.
Таблица 1.3
| Производящие отрасли |
Потребляющие отрасли |
Конечный продукт (Y) |
Валовой продукт (Х) |
|||
|
1 |
2 |
3 |
4 |
|||
|
1 |
203,33 |
36,26 |
142,70 |
124,99 |
700 |
1207,28 |
|
2 |
63,54 |
28,20 |
33,58 |
39,47 |
500 |
664,79 |
|
3 |
38,12 |
12,09 |
92,33 |
98,68 |
850 |
1091,22 |
|
4 |
241,46 |
4,03 |
8,39 |
124,99 |
700 |
1078,87 |
|
Чистая продукция (Z) |
660,83 |
584,21 |
814,22 |
690,74 |
||
|
Валовой продукт (Х) |
1207,28 |
664,79 |
1091,22 |
1078,87 |
||
Проверка: ![]() .
.
Построение графиков. Исследование статистических функций
Задание 1. Построить график плотности распределения хи-квадрат, протабулировав эту функцию на отрезке от 0 до 10 с шагом 0,2 и взяв степень
свободы k=5. Проанализировать зависимость параметра распределения k на график.
Решение:
Для построения графика функции, зададим значения аргумента х по формуле:
![]() , где i=0,…,n-1, х0=0.
, где i=0,…,n-1, х0=0.
Значения функции плотности распределения хи-квадрат находим с помощью функции MS Excel «ХИ2РАСП».
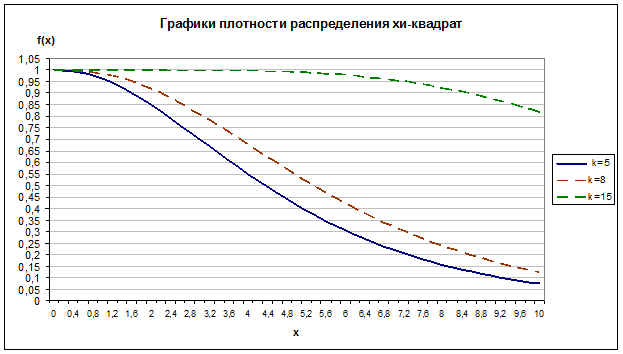
Рис. 2.1
Проследим как влияет параметр распределения k на график. Для этого построим дополнительно два графика для k=8 и k=15 (при этом же изменении аргумента).
Из рис. 2.1 видим, что с ростом значения параметра k происходит растяжение графика вдоль оси Ох, т.е. на одном и том же отрезке график функции с большим значением параметра более пологий.
Задание 2. Построить график плотности распределения Стьюдента, протабулировав эту функцию на отрезке от 0 до 7 с шагом 0,2 и взяв степень
свободы k=4. Проанализировать зависимость параметра распределения k на график.
Решение:
Значения функции плотности распределения Стьюдента находим с помощью функции MS Excel «СТЬЮДРАСП».
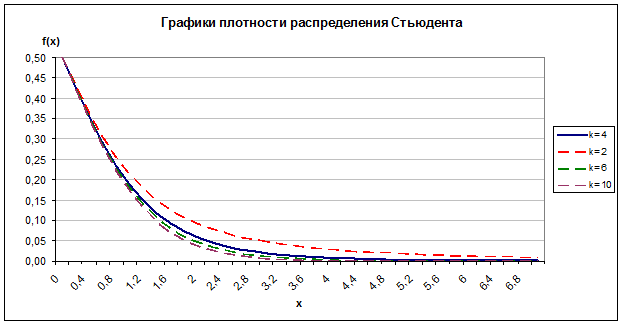
Рис. 2.2
Из рис. 2.2 видим, что с ростом значения параметра k график становится более вогнутый.
Задание 3. Построить график плотности распределения Фишера, протабулировав эту функцию на отрезке от 0 до 5 с шагом 0,2 и взяв степени
свободы m=4 и n=5. Проанализировать зависимость параметров распределения m и n на график.
Решение:
Значения функции плотности распределения Фишера находим с помощью функции MS Excel «FРАСП».
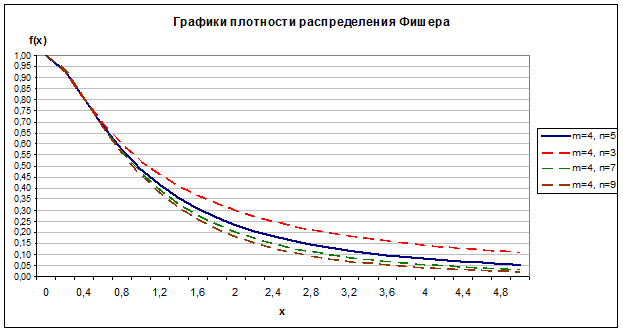
Рис. 2.3
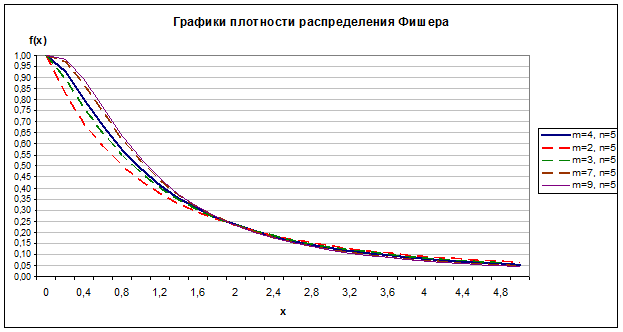
Рис. 2.4
Влияние параметров распределения m и n на график отображено на рис. 2.3 и 2.4.
Статистические методы обработки данных
Задание. Дана выборка выручки магазина за последние 30 дней. Составить статистический ряд, построить гистограмму, полигон, кумуляту.
| 70 |
59 |
57 |
62 |
49 |
63 |
59 |
60 |
57 |
66 |
64 |
57 |
59 |
58 |
59 |
|
56 |
62 |
56 |
57 |
63 |
59 |
55 |
58 |
62 |
61 |
60 |
59 |
59 |
61 |
63 |
Решение:
Построим интервальный статистический ряд. Оптимальное число интервалов определим по формуле Стерджесса:
![]() округляем до 6
округляем до 6
Ширину интервала разбиения рассчитываем по формуле:
![]()
Записываем интервальный статистический ряд:
| Интервал |
49-52,5 |
52,5-56 |
56-59,5 |
59,5-63 |
63-66,5 |
66,5-70 |
|
Частота |
1 |
3 |
13 |
10 |
2 |
1 |
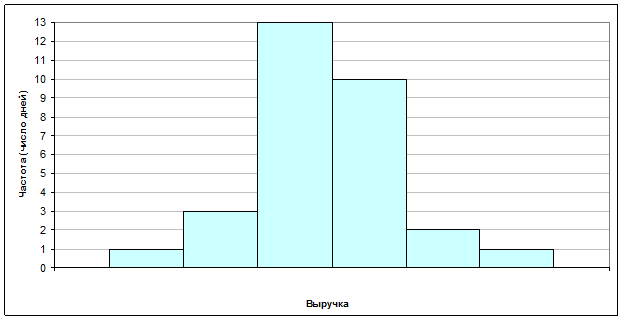
49 52,5 56 59,5 63 66,5 70
Рис. 3.1. Гистограмма
Построим полигон – ломаную кривую, соединяющую последовательно (в порядке возрастания значения абсциссы) точки, абсцисса которой равна середине интервала, а ордината – частоте попадания в интервал.
|
Интервал |
49-52,5 |
52,5-56 |
56-59,5 |
59,5-63 |
63-66,5 |
66,5-70 |
|
Середина интервала |
50,75 |
54,25 |
57,75 |
61,25 |
64,75 |
68,25 |
|
Частота |
1 |
3 |
13 |
10 |
2 |
1 |
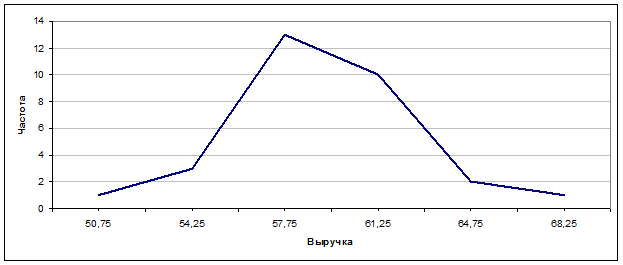
Рис. 3.2. Полигон
Для построения кумуляты рассчитаем накопленные частоты. Расчеты оформим во вспомогательной таблице.
| xi |
49 |
52,5 |
56 |
59,5 |
63 |
66,5 |
70 |
|
Частоты ni |
0 |
1 |
3 |
13 |
10 |
2 |
1 |
|
Накопленные частоты |
0 |
1 |
4 |
17 |
27 |
29 |
30 |
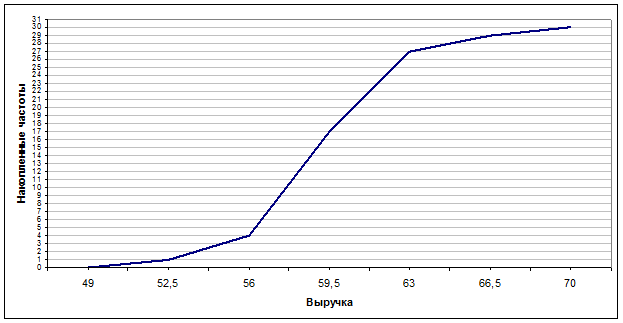
Рис. 3.3. Куммулята
Точечное и интервальное оценивание параметров распределений
Задание 1. Дана выборка выручки магазина за последние 30 дней. Вычислить объем выборки, выборочное среднее, дисперсию, стандартное отклонение, медиану, моду, коэффициент эксцесса, коэффициент асимметрии, перцентиль 60%, перцентиль 90%.
| 44 |
44 |
46 |
45 |
49 |
44 |
47 |
47 |
36 |
37 |
35 |
40 |
35 |
39 |
41 |
|
34 |
38 |
42 |
44 |
42 |
35 |
43 |
45 |
39 |
33 |
39 |
45 |
47 |
41 |
45 |
Решение:
Расчет указанных показателей осуществим с помощью встроенных функций MS Excel.
| Показатель |
Обозначение |
Числовое значение |
Расчетная формула |
| Объем выборки |
n |
30 |
=СЧЕТ(A3:O4) |
| Выборочное среднее |
|
41,37 |
=СРЗНАЧ(A3:O4) |
| Дисперсия |
S2 |
20,10 |
=ДИСП(A3:O4) |
| Стандартное отклонение |
s |
4,48 |
=СТАНДОТКЛОН(A3:O4) |
| Медиана |
Ме |
42 |
=МЕДИАНА(A3:O4) |
| Мода |
Мо |
44 |
=МОДА(A3:O4) |
| Коэффициент эксцесса |
Ех |
-1,031333 |
=ЭКСЦЕСС(A3:O4) |
| Коэффициент асимметрии |
As |
-0,2983144 |
=СКОС(A3:O4) |
| Перцентиль 60% |
44 |
=ПЕРСЕНТИЛЬ(A3:O4;0,6) | |
| Перцентиль 90% |
47 |
=ПЕРСЕНТИЛЬ(A3:O4;0,9) |
Задание 2. Для данных из задания 1 вычислить доверительные интервалы для математического ожидания и дисперсии при ? = 0,01. Изменяя значение уровня значимости ? сделать вывод о его влиянии на ширину интервала.
Решение:
Доверительный интервал для оценки математического ожидания в генеральной совокупности определим по формуле:
![]() ,
,
где ![]() определяется из формулы:
определяется из формулы: ![]() .
.
При ![]() имеем:
имеем: ![]() . По таблице значений функции Лапласа находим, что Ф(2,58)=0,495, следовательно,
. По таблице значений функции Лапласа находим, что Ф(2,58)=0,495, следовательно, ![]() .
.
В задании 1 было найдено (с точностью до 10-2): ![]() ,
, ![]() , n=30.
, n=30.
![]()
![]()
Изменяя значение уровня значимости ? сделаем вывод о его влиянии на ширину интервала.
При ![]() имеем:
имеем: ![]() . По таблице значений функции Лапласа находим, что Ф(3,29)=0,4995, следовательно,
. По таблице значений функции Лапласа находим, что Ф(3,29)=0,4995, следовательно, ![]() . Тогда
. Тогда
![]()
![]()
При ![]() имеем:
имеем: ![]() . По таблице значений функции Лапласа находим, что Ф(1,65)=0,45, следовательно,
. По таблице значений функции Лапласа находим, что Ф(1,65)=0,45, следовательно, ![]() . Тогда
. Тогда
![]()
![]()
Вывод: при уменьшении уровня значимости ширина доверительного интервала для математического ожидания увеличивается; при увеличении уровня значимости – ширина доверительного интервала уменьшается.
Доверительный интервал для дисперсии определяется по формуле:
![]() ,
,
где ![]() — значение функции «хи-квадрат» при доверительной вероятности
— значение функции «хи-квадрат» при доверительной вероятности ![]() и числе степеней свободы r=n-1;
и числе степеней свободы r=n-1;
![]() — значение функции «хи-квадрат» при доверительной вероятности
— значение функции «хи-квадрат» при доверительной вероятности ![]() и числе степеней свободы r=n-1.
и числе степеней свободы r=n-1.
При ![]() и r=29 имеем:
и r=29 имеем:
![]()
![]()
![]()
![]()
![]()
![]()
Изменяя значение уровня значимости ? сделаем вывод о его влиянии на ширину интервала.
При ![]() и r=29 имеем:
и r=29 имеем:
![]()
![]()
![]()
![]()
![]()
![]()
При ![]() им и r=29 имеем:
им и r=29 имеем:
![]()
![]()
![]()
![]()
![]()
![]()
Вывод: при уменьшении уровня значимости ширина доверительного интервала для дисперсии увеличивается; при увеличении уровня значимости – ширина доверительного интервала уменьшается.
Ответ: при уровне надежности ? = 0,01 ![]() — доверительный интервал для математического ожидания;
— доверительный интервал для математического ожидания; ![]() — доверительный интервал для дисперсии.
— доверительный интервал для дисперсии.
При уменьшении уровня значимости ширина доверительного интервала как для мат. ожидания, так и для дисперсии увеличивается; при увеличении уровня значимости – ширина доверительного интервала уменьшается.
Проверка статистических гипотез о виде распределения
Задание 1. Дана выборка числа посетителей Интернет – сайта за 30 дней. Проверить по критерию Пирсона на уровне значимости ? = 0,02 статистическую гипотезу о том, что генеральная совокупность, представленная выборкой, имеет нормальный закон распределения.
| 15 | 31 | 26 | 34 | 31 | 30 | 28 | 36 | 35 | 33 | 25 | 35 | 33 | 30 | 27 |
| 19 | 23 | 28 | 25 | 25 | 41 | 29 | 24 | 17 | 18 | 28 | 30 | 31 | 31 | 31 |
Решение:
Составим интервальный вариационный ряд.
Построим интервальный статистический ряд. Оптимальное число интервалов определим по формуле Стерджесса:
![]() округляем до 6
округляем до 6
Ширину интервала разбиения рассчитываем по формуле:
![]()
Записываем интервальный статистический ряд:
| Интервал |
15-19,3 |
19,3-23,7 |
23,7-28 |
28-32,3 |
32,3-36,7 |
36,7-41 |
|
Частота |
4 |
1 |
9 |
9 |
6 |
1 |
По исходным данным выборки с помощью встроенных функций «СРЗНАЧ» и «СТАНДОТКЛОН» рассчитаем выборочную среднюю и среднее квадратическое отклонение:
![]()
Произведем проверку статистической гипотезу о том, что генеральная совокупность, представленная выборкой, имеет нормальный закон распределения с помощью критерия согласия Пирсона (уровень значимости ![]() .
.
Вычислим наблюдаемое значение критерия Пирсона:
![]()
![]()
n=30![]()
![]()
![]()
![]()
Значения функции Лапласа вычислим, используя встроенную функцию MS Excel «НОРМРАСП» с помощью формулы:
![]()
Оформим расчеты в таблице.
Таблица 5.1
| хi |
xi+1 |
|
|
Ф(zi) |
Ф(zi+1) |
Pi |
n/i |
ni |
|
|
15 |
19,3 |
-2,247 |
-1,520 |
-0,4877 |
-0,4358 |
0,0519 |
1,56 |
4 |
3,835 |
|
19,3 |
23,7 |
-1,520 |
-0,777 |
-0,4358 |
-0,2814 |
0,1543 |
4,63 |
1 |
2,846 |
|
23,7 |
28 |
-0,777 |
-0,051 |
-0,2814 |
-0,0202 |
0,2612 |
7,84 |
9 |
0,173 |
|
28 |
32,3 |
-0,051 |
0,676 |
-0,0202 |
0,2504 |
0,2706 |
8,12 |
9 |
0,096 |
|
32,3 |
36,7 |
0,676 |
1,419 |
0,2504 |
0,4220 |
0,1717 |
5,15 |
6 |
0,140 |
|
36,7 |
41 |
1,419 |
2,145 |
0,4220 |
0,4840 |
0,0620 |
1,86 |
1 |
0,397 |
|
Сумма |
7,488 |
![]()
Рассчитываем в MS Excel критическое значение ![]() для уровня значимости
для уровня значимости ![]() и числа степеней свободы k=s-3=6-3=3 (s — число интервалов) находим
и числа степеней свободы k=s-3=6-3=3 (s — число интервалов) находим ![]() .
.
Так как ![]()
![]() , то гипотезу о нормальном распределении принимаем.
, то гипотезу о нормальном распределении принимаем.
Ответ: на 2% уровне значимости статистическая гипотеза о том, что генеральная совокупность, представленная выборкой, имеет нормальный закон распределения, подтверждается.
Задание 2. При производстве микросхем процессоров используются кристаллы кварца. Стандартом предусмотрено, чтобы у 50 % образцов не было обнаружено ни одного дефекта кристаллической структуры, у 15% — один дефект, у 13 % — 2 дефекта, у 12 % — 3 дефекта, у 10 % более 3 дефектов.
При анализе выборочной партии оказалось, что из 1000 экземпляров распределение по дефектам имеет распределение, указанное в таблице:
| 0 дефектов |
1 дефект |
2 дефекта |
3 дефекта |
более 3 |
|
471 |
159 |
135 |
127 |
108 |
Можно ли с вероятностью 0,99 (при ? = 0,01) считать, что партия соответствует стандарту?
Решение:
Вычислим наблюдаемое значение критерия Пирсона:
![]()
ni – теоретические частоты (в случаях, предусмотренных стандартом);
![]() — эмпирические частоты.
— эмпирические частоты.
Таблица 5.2
| № п/п |
ni |
n/i |
|
|
1 |
500 |
471 |
1,786 |
|
2 |
150 |
159 |
0,509 |
|
3 |
130 |
135 |
0,185 |
|
4 |
120 |
127 |
0,386 |
|
5 |
100 |
108 |
0,593 |
|
Сумма |
|
|
3,459 |
![]()
Рассчитываем в MS Excel критическое значение ![]() для уровня значимости
для уровня значимости ![]() и числа степеней свободы k=s-1=5-1=4 (s — число групп) находим
и числа степеней свободы k=s-1=5-1=4 (s — число групп) находим ![]() .
.
Так как ![]()
![]() , то гипотеза о соответствии СТАНДАРТУ проверенной партии образцов микросхем подтверждается.
, то гипотеза о соответствии СТАНДАРТУ проверенной партии образцов микросхем подтверждается.
Ответ: с вероятностью 0,99 можно считать, что партия соответствует стандарту.
Проверка гипотезы о равенстве дисперсий
Задание. Четыре станка в цеху обрабатывают детали. Для проверки точности обработки взяли выборки размеров деталей у каждого станка.
Необходимо сравнить с помощью F-теста попарно точности обработки всех станков (рассмотреть пары 1-2, 1-3, 1-4, 2-3, 2-4, 3-4) и сделать вывод, для каких станков точности обработки (дисперсии) равны, для каких нет. Взять уровень значимости ? = 0,02 .
| 1 станок |
36,6 |
34,3 |
33,9 |
30,3 |
30 |
31,4 |
29,9 |
26,8 |
24,7 |
32,5 |
|
2 станок |
28,4 |
32,5 |
31,5 |
28,2 |
33,9 |
24,7 |
31,7 |
29,7 |
30,1 |
28 |
|
3 станок |
33,1 |
30,4 |
33,4 |
29,6 |
27,7 |
33,2 |
28,3 |
31,6 |
31,6 |
29,1 |
|
4 станок |
30,6 |
31,6 |
29,3 |
26,3 |
33,8 |
29,1 |
26,1 |
32,3 |
32,4 |
31,3 |
Решение:
Будем рассматривать пары 1-2, 1-3, 1-4, 2-3, 2-4, 3-4.
Обозначим через Х – первую выборку в паре, через Y – вторую выборку в паре.
Основная (нулевая) гипотеза Н0: D(Х)=D(Y).
Альтернативная (конкурирующая) гипотеза Н1: D(Х)![]() D(Y).
D(Y).
Для каждой из выборок Х и Y рассчитываем исправленные дисперсии S2 с помощью встроенной функции MS Excel «ДИСП» и далее рассчитываем наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей):
![]() .
.
С помощью MS Excel рассчитываем критическое значение критерия:
![]() ,
,
где ![]() ,
, ![]() — степени свободы.
— степени свободы.
В данной задаче ![]() . Тогда
. Тогда ![]() .
.
Если ![]() , то нулевую гипотезу о равенстве дисперсий принимаем. Если
, то нулевую гипотезу о равенстве дисперсий принимаем. Если ![]() , то нулевую гипотезу о равенстве дисперсий отвергаем и принимаем альтернативную гипотезу.
, то нулевую гипотезу о равенстве дисперсий отвергаем и принимаем альтернативную гипотезу.
Таблица 6.1
|
Исправленная дисперсия |
|||||||||||
|
1 станок |
36,6 |
34,3 |
33,9 |
30,3 |
30 |
31,4 |
29,9 |
26,8 |
24,7 |
32,5 |
12,56 |
|
2 станок |
28,4 |
32,5 |
31,5 |
28,2 |
33,9 |
24,7 |
31,7 |
29,7 |
30,1 |
28 |
7,16 |
|
3 станок |
33,1 |
30,4 |
33,4 |
29,6 |
27,7 |
33,2 |
28,3 |
31,6 |
31,6 |
29,1 |
4,38 |
|
4 станок |
30,6 |
31,6 |
29,3 |
26,3 |
33,8 |
29,1 |
26,1 |
32,3 |
32,4 |
31,3 |
6,61 |
Таблица 6.2
| Пара |
Наблюдаемое значение F-критерия Fнабл |
Критическое значение F-критерия Fкр |
Проверка выполнения условия: Fнабл<Fкр |
Вывод о принятии гипотезы |
|
1-2 |
1,755 |
4,33 |
выполняется |
Н0 принимаем |
|
1-3 |
2,867 |
выполняется |
Н0 принимаем |
|
|
1-4 |
1,900 |
выполняется |
Н0 принимаем |
|
|
2-3 |
1,633 |
выполняется |
Н0 принимаем |
|
|
2-4 |
1,082 |
выполняется |
Н0 принимаем |
|
|
3-4 |
1,509 |
выполняется |
Н0 принимаем |
Вывод: для всех 4-х станков точности обработки (дисперсии) равны.
Проверка гипотезы о равенстве математических ожиданий
Задание. Имеются данные о количествах продаж товара в двух городах. Проверить на уровне значимости 0,01 статистическую гипотезу о том, что среднее число продаж товара в городах различно.
| Первый город | |||||||||||||
|
23 |
25 |
23 |
22 |
23 |
24 |
28 |
16 |
18 |
23 |
29 |
26 |
31 |
19 |
|
Второй город |
|||||||||||||
| 21 | 28 | 18 | 30 | 27 | 24 | 28 | 28 | 22 | 26 | 27 | 26 | ||
Решение:
Используем пакет «Анализ данных». В зависимости от типа критерия выбирается один из трех: «Парный двухвыборочный t-тест для средних» — для связных выборок, и «Двухвыборочных t-тест с одинаковыми дисперсиями» или «Двухвыборочных t-тест с разными дисперсиями» — для несвязных выборок.
Вызовем тест с одинаковыми дисперсиями, в открывшемся окне в полях «Интервал переменной 1» и «Интервал переменной 2» вводим ссылки на данные (А1-N1 и А2-L2, соответственно).
Если имеются подписи данных, то ставится флажок у надписи «Метки» (у нас их нет, поэтому флажок не ставится).
Далее вводим уровень значимости в поле «Альфа» — 0,01.
Поле «Гипотетическая средняя разность» оставляем пустым.
В разделе «Параметры вывода» ставим метку около «Выходной интервал» и поместив курсор в появившемся поле напротив надписи, щелкаем левой кнопкой в ячейке В4. Вывод результата будет осуществляться начиная с этой ячейки.
Процедура выводит основные характеристики выборки, t-статистику, критические значения этих статистик и критические уровни значимости «Р(Т<=t) одностороннее» и «Р(Т<=t) двухстороннее». Если по модулю t-статистика меньше критического, то средние показатели с заданной вероятностью равны.
Таблица 7.1
Результаты двухвыборочного t-теста с одинаковыми дисперсиями
|
|
Город 1 |
Город 2 |
| Среднее |
23,5714 |
25,4167 |
| Дисперсия |
17,3407 |
12,2652 |
| Наблюдения |
14 |
12 |
| Объединенная дисперсия |
15,0144 |
|
| Гипотетическая разность средних |
0 |
|
| df |
24 |
|
| t-статистика |
-1,2105 |
|
| P(T<=t) одностороннее |
0,1189 |
|
| t критическое одностороннее |
2,4922 |
|
| P(T<=t) двухстороннее |
0,2379 |
|
| t критическое двухстороннее |
2,7969 |
Так как ¦-1,2105¦ < 2,7969, следовательно, среднее число продаж значимо не отличается.
Ответ: на 1% уровне значимости статистическая гипотеза о том, что среднее число продаж товара в городах различно не подтверждается.
Основы регрессионного и корреляционного анализа
Некоторая фирма, производящая товар, хочет проверить, эффективность рекламы этого товара. Для этого в 10 регионах, до этого имеющих одинаковые средние количества продаж, стала проводиться разная рекламная политика и на рекламу начало выделяться xi денежных средств.
При этом фиксировалось число продаж yi.
Задание. По этим выборкам найти уравнение линейной регрессии ![]() = ax + b. Найти коэффициент парной корреляции. Проверить на уровне значимости ? = 0,05 регрессионную модель на адекватность.
= ax + b. Найти коэффициент парной корреляции. Проверить на уровне значимости ? = 0,05 регрессионную модель на адекватность.
| Расходы на рекламу хi, млн. руб. | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| Объем продаж уi | 25,3 | 28,8 | 30,1 | 30 | 32,5 | 31,4 | 32 | 36,4 | 35,6 | 36,9 |
Решение:
Используем инструмент «Регрессия» пакета «Анализ данных» MS Excel.
Таблица 8.1
Результаты регрессионного моделирования
| Регрессионная статистика | ||||||
| Множественный R |
0,948 |
|||||
| R-квадрат |
0,899 |
|||||
| Нормированный R-квадрат |
0,887 |
|||||
| Стандартная ошибка |
1,226 |
|||||
| Наблюдения |
10 |
|||||
| Дисперсионный анализ | ||||||
|
|
df |
SS |
MS |
F |
Значи—мость F |
|
| Регрессия |
1 |
107,56 |
107,56 |
71,58 |
0,00003 |
|
| Остаток |
8 |
12,02 |
1,50 |
|||
| Итого |
9 |
119,58 |
||||
|
|
Коэффи—циенты |
Стандарт—ная ошибка |
t-статис—тика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
Y-пересечение |
26,76 |
0,72 |
37,14 |
0,00000000 |
25,10 |
28,42 |
|
Переменная X 1 |
2,28 |
0,27 |
8,46 |
0,00002912 |
1,66 |
2,91 |
Коэффициент b – это коэффициент при «Y-пересечение», т.е. b=26,76.
Коэффициент а – это коэффициент при «Переменная X 1», т.е. a=2,28.
Уравнение линейной регрессии имеет вид: ![]() = 2,28x +26,76.
= 2,28x +26,76.
Найдем коэффициент парной корреляции.
Для этого используем встроенную функцию MS Excel «КОРРЕЛ».
![]() .
.
Значение коэффициента парной корреляции положительно и близко к 1, что говорит об очень тесной прямой связи между рассматриваемыми показателями, т.е. с увеличением расходов на рекламу объем продаж так же растет.
Проверим на уровне значимости ? = 0,05 регрессионную модель на адекватность с помощью F-критерия Фишера.
Рассчитаем фактическое значение F-критерия по формуле:
![]() ,
,
или определяем из таблицы 8.1.
![]()
С помощью встроенной функции «FРАСПОБР» MS Excel для уровня значимости ![]() и числа степеней свободы k1=1 и k2=n-2=10-2=8 находим критическое значение критерия Fкр.
и числа степеней свободы k1=1 и k2=n-2=10-2=8 находим критическое значение критерия Fкр.
![]()
Если окажется что ![]() , то это означает, что гипотеза о несущественности связи между Y и Х с вероятностью ошибочности суждения
, то это означает, что гипотеза о несущественности связи между Y и Х с вероятностью ошибочности суждения ![]() отклоняется, т.е. связь между этими переменными может быть признана существенной, а модель в целом статистически значимой (адекватной).
отклоняется, т.е. связь между этими переменными может быть признана существенной, а модель в целом статистически значимой (адекватной).
![]() , следовательно, полученная модель линейной регрессии адекватна.
, следовательно, полученная модель линейной регрессии адекватна.



