- Есть вопросы?
- 8(961)1155384
- zakaz@kursach37.com
Экономико-математическое моделирование
Задание 1. Решить графически задачу линейного программирования
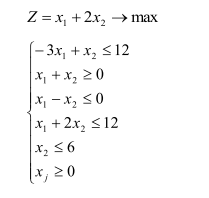
Задание 2. Построить математическую модель задачи
Имеется два вида продуктов питания А и В, каждый из которых содержит белки, жиры и углеводы. Количественный состав этих продуктов и их цен заданы таблицей.
| Состав | Продукт | |
| А | В | |
| Белки | 3 | 3 |
| Жиры | 2 | 1 |
| Углеводы | 3 | 8 |
| Цена | 4 руб. | 6 руб. |
Минимальная потребность в питательных веществах — белках, жирах, углеводах соответственно 45, 10, 60 единиц, при этом можно потребить продукта А не более 25 единиц, а продукта В — не более 30 единиц. Требуется рассчитать необходимое количество обоих продуктов так, что бы удовлетворить потребность организма в указанных веществах при минимальных денежных затратах.
Задание 3. Решить задачу линейного программирования симплексным методом
Предприятие выпускает два вида продукции А и В, для производства которых используется сырье трех типов. На изготовление единицы изделия А требуется затратить сырья каждого типа а1, а2, а3 кг соответственно, а для единицы изделия В — b1, b2, b3 кг. Производство обеспечено сырьем каждого типа в количестве p1, p2, p3 кг, соответственно. Прибыль от реализации единицы изделия А составляет руб., а единицы изделия В — руб. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
| a1 = 1
a2 = 4 a3 = 3 |
b1 = 4
b2 = 3 b3 = 4 |
р1 = 353
р2 = 484 р3 = 440 |
α = 5
β = 10 |
Задание 5
Однородный груз сосредоточен у трех поставщиков в объемах a1, a2 , a3. Данный груз необходимо доставить четырем потребителям, потребности которых составляют b1, b2, b3, b4 соответственно. Стоимости перевозок единицы груза заданы матрицей С. Требуется составить такой план перевозок, чтобы суммарные затраты на перевозку были минимальны.
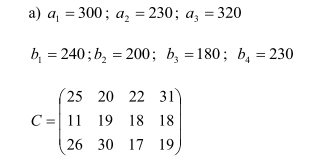
Содержание
1. Ильченко А.Н. Экономико-математические методы. – М.: Финансы и статистика, 2006.
2. Исследование операций в экономике: Учеб. пособие для вузов. /Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ , 2004.
3. Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике. Учебное пособие для вузов / Под ред. проф. Н.А. Орехова – М.: ЮНИТИ-ДАНА, 2004.
4. Шапкин А.С., Мазаева Н.П. математические методы и модели исследования операций. – М.: «Дашков и К0», 2006.
5. Экономико-математическое моделирование. Учебник для вузов / Под общ. ред. И.Н. Дрогобыцкого. – М.: Изд. «Экзамен», 2004.
Общий объем: 14
Год: 2018